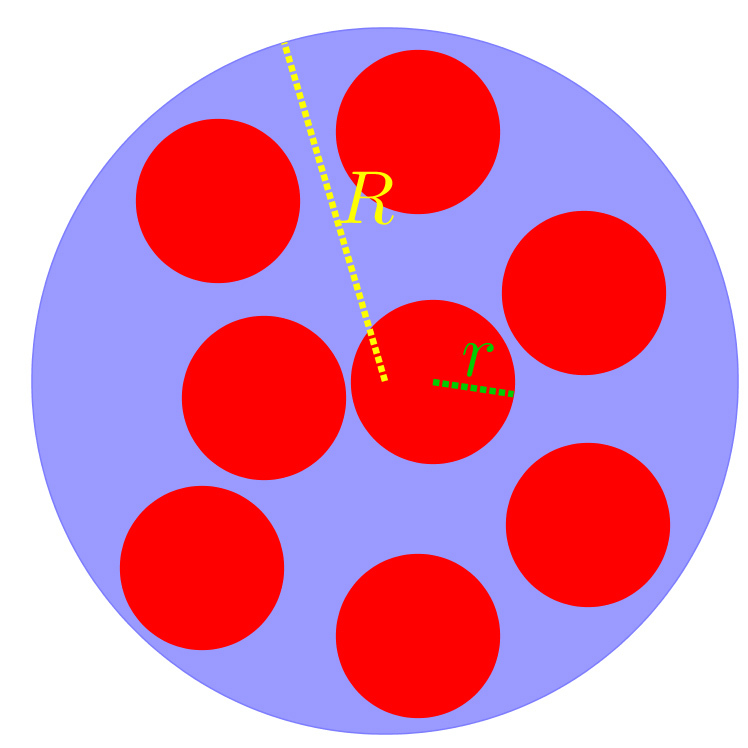
Loving circles

Geometry Level 3

In a circle with a radius of $R$ we placed $n$ number of circles with a radius of $r$ , so that

No two of them cover each other.
Neither of them hangs out of the circle

We know that we can't place one more circle with radius of $r$ with the conditions above. Which of the following statement is ture, if

$x=\sqrt{n}$

$y=\frac{R}{r}$

$z=\frac{1}{2}*\left(\frac{R}{r}-1\right)$ ?

A) $x<y<z$

B) $x<z<y$

C) $y<x<z$

D) $y<z<x$

E) $z<x<y$

F) $z<y<x$

D B E F C A

1 solution

Áron Bán-Szabó
Jun 12, 2017

The sum of the circles' area with radius of $r$ is less than the circle with radius of $R$ : $n*\pi*r^2<\pi*R^2$ , so $\sqrt{n}<\frac{R}{r}$ . No we multiply all of the circles' radiuses by two, so these cover the circle with radius of $R-r$ , so $\pi*n*(2r)^2>\pi*(R-r)^2$ , and from that we get

$\boxed{\frac{1}{2}*\left(\frac{R}{r}-1\right)<\sqrt{n}<\frac{R}{r}}$ .

Loving circles

1 solution

0 pending reports