Nice Geometry
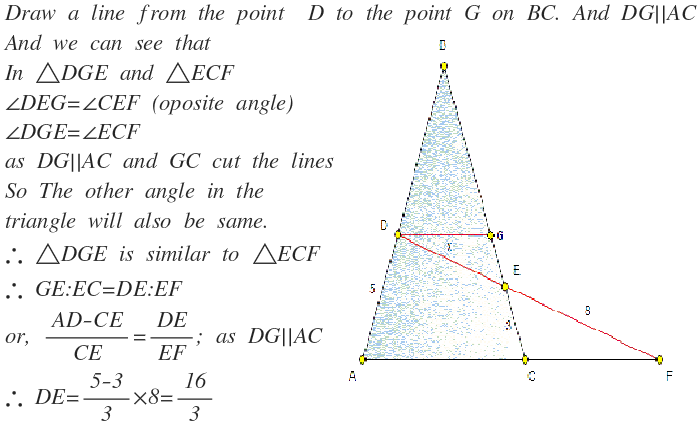
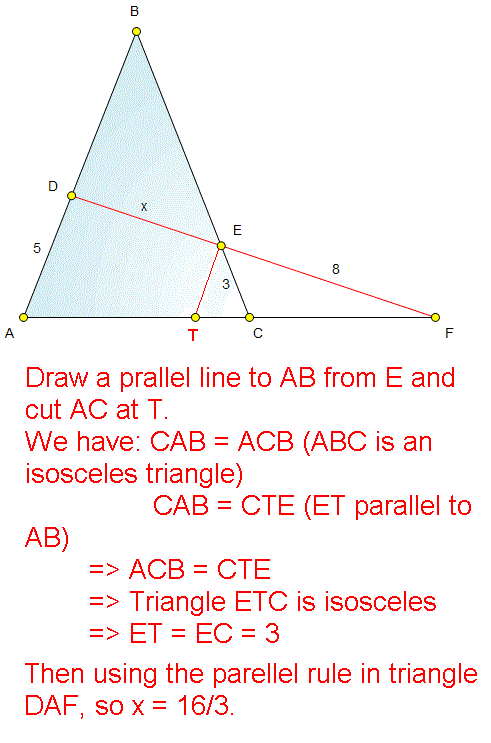
The figure shows an isosceles △ A B C with A B = B C . The line D E cuts A C extended at F . If A D = 5 , C E = 3 , and E F = 8 , find D E .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
great job! absolutely elegant!!!
Congratulations, very clever índeed. Using triangles similarity between ADF and TEF then (8+x)/5=8/3 I have reached the same outcome , but I used sinus. Your method is simpler so is better.
Banti Paswan..... your'e awesome !!!
better use similar triangle theorem.... draw a parallel line to AC first and then use theorem.. it will be easier...
Interesting problems, good solution
proud of indian
You make this looks complicated. Good job...

Đào Minh Tân's solution is more direct.
Put a point G between point A and C so that DG has a length of 5. Then, we have this ratio between lengths, since triangles DGF and ECF are similar:
(x+8)/5 = 8/3
then, cross multiply:
40 = 3x+24
Subtract 24...
3x = 16
... and divide by 3.
x = 16/3
Let ∠ C A B = α , and ∠ C F E = β ; then, it is true that ∠ F C E = 1 8 0 ∘ − α .
Firstly, applying the law of sines on △ A F D yields: x + 8 s i n α = 5 s i n β
We can write this as:
s i n β s i n α = 5 x + 8
Now, applying the law of sines on △ E F C yields: 3 s i n β = 8 s i n ( 1 8 0 ∘ − α )
Noting that s i n ( 1 8 0 ∘ − α ) = s i n α , we can write this as:
s i n β s i n α = 3 8
Thus:
5 x + 8 = 3 8
Solving for x gives us x = 3 1 6 .