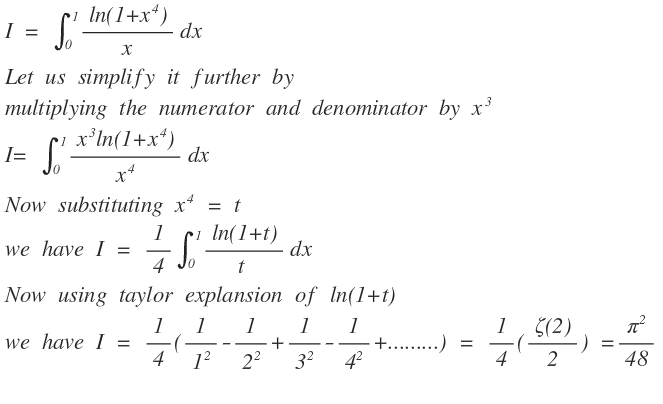Nice integral
∫ 0 1 x ln ( 1 + x 4 ) d x = B π A
If for positive integers A , B , the above integral satisfies, submit the value of ϕ ( B − A ) as your answer where ϕ ( s ) denotes the Euler-Totient Function.
The answer is 22.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Consider.
I
=
∫
0
1
x
ln
(
1
+
x
p
)
d
x
as,
ln
(
1
+
x
)
=
n
=
1
∑
∞
n
x
n
(
−
1
)
n
+
1
plugging
x
→
x
p
ln
(
1
+
x
p
)
=
n
=
1
∑
∞
n
x
n
p
(
−
1
)
n
+
1
Note that as the integral has the limits from
0
to
1
so the above series is valid.
Hence
I
=
∫
0
1
n
=
1
∑
∞
n
x
x
n
p
(
−
1
)
n
+
1
d
x
=
n
=
1
∑
∞
n
(
−
1
)
n
+
1
∫
0
1
x
n
p
−
1
d
x
=
n
=
1
∑
∞
p
n
2
(
−
1
)
n
+
1
The second step is verified by Fubini-Tonelli's theorem
By the fact that
n
=
1
∑
∞
n
2
(
−
1
)
n
+
1
=
1
2
π
2
Hence,
I
=
1
2
p
π
2
For our case , plug
p
=
4
, so
I
=
4
8
π
2
Clearly,
ϕ
(
4
8
−
2
)
=
ϕ
(
4
6
)
=
2
2
Q.E.D
Use series expansion of l n ( 1 + x ) yields the values as ζ ( 2 ) / 8 = I = π 2 / 4 8