nice number theory equation!
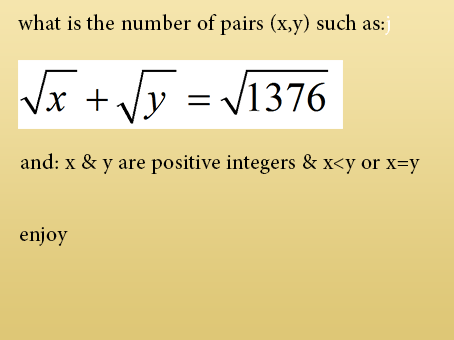what is the number of pairs (x,y) such as:
1)
2)
3) & are positive Integers.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Prime factorize 1376 2^5 * 43 So sqrt (1376)=4sqrt (86) Look at 4. If x+y=4, x <=y, {x, y} € II, you will notice the only pairs that satisfy are {1,3} and {2,2} So for the original problem we get {sqrt 86, 3 sqrt 86} and {2 sqrt 86, 2 sqrt 86}