Nice to meet you
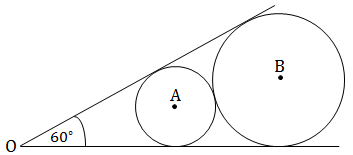
(Refer to diagram below) Two lines intersect at O at an angle of 6 0 ∘ . Two circles are drawn such that they are tangent to each other and the two lines. A and B are the centers of the smaller and larger, respectively. If the radius of the smaller circle is 1 5 , what is the length of O B ?
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
24 solutions
We will first show that the points O, A, and B all lie on the same line, which is at an angle of 30 degrees above the horizontal.
Consider a circle (with center C) tangent to the two lines in the above drawing. Let D and E be the upper and lower points of tangency, respectively. Draw line segments CD and CE such that we have two right triangles: ODC and OCE with right angles ∠ O D C and ∠ O E C . These triangles are congruent by RHS (they share a hypotenuse, one of the sides is the radius of circle C, and they both have 90 degree angles). Hence, ∠ D O C and ∠ C O E are equal, and since they sum to 60 degrees, each has measure 30 degrees.
Since this result holds for any circle tangent to the two lines above, we conclude that O, A, and B lie on the same line at 30 degrees to the horizontal.
Now draw this line and let Q and P be the lower points of tangency of the smaller circle and the larger circle, respectively. Also let r be the radius of the larger circle. From triangle OAQ, we have sin ( 3 0 ∘ ) = 0 . 5 = O A 1 5 , from which O A = 3 0 .
Now, from triangle OBP, we have:
sin ( 3 0 ∘ ) = 0 . 5 = O A + 1 5 + r r = 3 0 + 1 5 + r r .
Solving this equation for r , we get r = 4 5 .
And so O B = 3 0 + 1 5 + 4 5 = 9 0
Let the tangential points of circles A and B to one of the lines be Q and R respectively such that ∠ A Q O = ∠ B R O = 9 0 ∘ . OA bisects angle O so that ∠ A O Q = 3 0 ∘ . In a 3 0 ∘ − 6 0 ∘ − 9 0 ∘ triangle, the ratio of base : altitude : hypotenuse is 1 : 2 : 3 . With A Q = 1 5 as the base of triangle AOQ, O A = 3 0 . Triangles AOQ and BOR are similar, so 3 0 1 5 = 4 5 + x x and x = 4 5 . Therefore, O B = 3 0 + 1 5 + 4 5 = 9 0 .
Draw the line A C from center A to either tangent point of circle A to either line. Notice that ∠ A O C = 3 0 and ∠ A C O = 9 0 , therefore 2 A C = A O , and so A O = 3 0 . Now call the radius of circle B as x . By similar triangles, x 4 5 + x = 1 5 3 0 . Solving the proportion gives x = 4 5 . Now all we need to do is find B O . B O = 4 5 + 1 5 + 3 0 = 9 0 and we are done.
Drop a perpendicular A ′ from A to the tangent from O . Similarly, establish B ′ on the extension of O A ′ .
Since ∠ A O A ′ = 3 0 ∘ , we have sin 3 0 ∘ = 2 1 = O A 1 5 ⟹ O A = 3 0 .
O B = O A + A A ′ + B B ′ = 4 5 + B B ′
Similarly, sin 3 0 ∘ = O B B B ′ = 4 5 + B B ′ B B ′ = 2 1 .
B B ′ > 0 ⟹ O B = 4 5 + B B ′ = 9 0
The hypotenuse of a right triangle is the double of the size of the cathetus that is opposite to the angle of 30 degrees. Then we can say that: (R = larger radius; r = smaller radius)
OA = 2r = 30
OB = 2R = R + 3r = 6r = 90
Radii from A & B that intersect the tangent lines from O form right angles. Let a radius from A intersect the diagonal line at C. Let a radius from B intersect the diagonal line at D. Bisecting angle O creates 30-60-90 triangles. Since AC = 15, then OC = 15\sqrt{3}, and OA = 30. Representing the radius of circle B as x: BD = x, OB = 30 + 15 + x = 45 + x. Because OBD and OAC are similar triangles (proven by the fact that 2 corresponding angles of each triangle have the same measure), OBD is also a 30-60-90 triangle. This means that OB = 2(BD). 45 + x = 2x x = 45 OB = 90
Denote one of the lines through O as L. Denote the circle with center A as X. Denote the circle with center B as Y. Denote the intersection of L and X as C. Denote the intersection of L and Y as D. AC = 15. L is tangent to A at C. L is tangent B at D. OA bisects the 60 degree angle. angle AOC = 30 degrees. Triangle AOC and triangle BOD are 30-60-90 triangles. OA = 30. Triangle AOC and triangle BOD are similar. AC / OA = BD / OB. OB = OA + AC + BD. Therefore, 1/2 = BD / (45 + BD). BD = 45. OB = 90.
Let the tangents to the circle centered at A be at points C and D. And let these tangents meet the circle centered at B be at points E and F.
We know that the length OC = OD and AC = AD = 15(radius of small circle) and OA is the third common side Hence the triangles OAC and OAD are similar.
Hence the angle AOC = AOD = 6 0 ∘ / 2 = 3 0 ∘
Similarly we can prove that OBE and OBF are similar triangles. Hence O,A and B lie on the same line.
Let the distance from O to A be x We already know that AC = radius = 15 Angle ABC = 3 0 ∘ sin ( 3 0 ∘ ) = 1 / 2
We know that 1 5 / ( x + 1 5 ) = 1 / 2 Solving for x we get x as 15 Now solving for the radius of larger circle using s i n ( 3 0 ∘ ) ( 4 5 + r ) / r = s i n ( 3 0 ∘ ) = 1 / 2 we get r as 45 Hence the length OB = 15 + 2 smaller circle radius + larger circle raduies = 15 + 2 15 + 45 = 90
Assume 2 points of the line that tangent Circle A and Circle B as X and Y.
Because the line and the circles are tangent, then the angles of AXO and BYO are 90.
Using sinus rule, AX/AO = sin 30 = 1/2.
AX = 15 (because AX is the radius of Circle A), so AO = 30.
Assume BY = r2, and the point that tangent Circle A and Circle B called Z, so AX = AZ = 15, and BY = BZ = r2.
BO = AO + AZ + BZ = 30 + 15 + r2.
Using sinus rule again, BY/BO = sin 30 = 1/2, so BO = 2 BY = 2 (r2).
45 + r2 = 2*(r2), so r2 = 45.
BO = 2*(r2) = 90...
First add O and B . So A point will be on that line. Suppose C and D are the feet of the perpendiculars from A and B to the upper line. And E and F are the feet of the perpendiculars from A and B to the lower line. Now look, \angle OCA + \angle OEA = 180 ^ \circ. So O, E, A and C are con-cyclic. And in that circle, AC and AE are the equal arc. So, \angle AOC = \angle AOE = 30 ^ \circ. In that same way, \angle BOD = \angle BOF = 30 ^ \circ. Now, in the right angled triangles OAC and OBD, two acute angles, \angle AOC = \angle BOD = 30 ^ \circ. So the two triangles are simialr. And, in the right angled triangle OAC, \sin \angle AOC = \frac {AC}{AO}. or, sin 30^\circ = \frac {AC}{AO}. or, .5 = \frac {AC}{AO}. or, AO= 2 \times AC = 30. Now, suppose the radius of the larger circle is x. So, OB= 30 + 15 + x = 45+x. Now look, in the similar triangles AOC and BOD, \frac {AC}{OA} = \frac {BD}{OB}. or, \frac {15}{30} = \frac {x}{45+x}. or, \frac {x}{45+x} = .5. or, 45+ x = 2x. or, 2x - x =x =45. So, OB= 45 + x = 45+45 =90. And that is the answer. Ans.: 90. Sorry for poor English.
Constructing AT and RB such T and R are points of tangencies of the circles and line, and contruct also SQ such that Q is the point of tangency of the two circles and S is contained in OR. Since OB contains the center of the circle, then angle ROB is 30 degrees. Using the concept of 30 -60 – 90 triangle. The smaller circle has radius of 15, so OA is 30. Therefore OQ is 45. Since SQ is perpendicular to OB therefore OS is 30 times the square root of 3, half of OS is equal to SQ. Considering TA and SQ we can obtain RB by multiplying square root of 3 to SQ, so RB is 45, thus OB is 90 since it is the hypotenuse of triangle ORB.
Let circles A and B touch the tangent at D and E(both on same tangent). Now, AD/OA= Sin 30(in triangle OAD). Hence OA= 30cm(Since AD=15cm). Now, in triangle OEB, Sin30=BE/OB = r/(45+r)=1/2.( here 'r' is the radius of circle B). Upon solving, we get r=45cm. Hence, OB= OA+AB=90cm .
radius of small circle to the tangent is 15. I have a right triangle now. Also OA divides angle to the half, so it is 30 degrees. From the formula, sin30=opposite/hypotenuse sin30=15/OA, so OA = 15 / 0.5 = 30
Distance OA + radius of small circle = 45
Now, I want to find the length OB Radius of big circle to the tangent line makes again a right triangle. Let x = radius of the big circle. I have again the formula sin30 = opposite / hypotenuse opposite = x hypotenuse = distance I found before (45) + x (radius of the big circle). So, sin30 = x / (45+x) 0.5 (45+x) = x 22.5 +0.5x =x 22.5 = 0.5 x so x =45 (radius of big circle)
So, length of OB = 45 + 45 = 90
Draw a perpendicular from A to the any of the tangent ,call it P..
Draw a line OA. it will be the angle bisector angle of angle POA and it will be equal to 30 degree. since lengths tangents from an external point are equal.
in triangle OPA sin30 gives OA to be 30 units.
Draw BQ perpendicular to any of the tangent.
again OB is the angle bisector of ANGLE QOB.
In triangle OBQ sin30 gives the relation OB=2R where R is the radius of the bigger circle.
now OB can be written as OA+ r+R where r is the radius of smaller circle=15
on solving we get R=45.
which gives OB=2*45=90 units.
Lets name the the two tangents as OX and OZ , respectively,
let the circles touch each other at piont P,
Now, draw a perpendicular from center A and from center B to the tangent OZ AC and BD respectively,
and join OA and OB, and this bisects \angle XOZ in \angle XOA and \angle AOC 30^\circ each,
we know that, \sin \theta = \frac {AC}{OA}
\Rightarrow \sin 30^\cric =\frac {15}{OA}
\Rightarrow OA= 30.......................................(1)
now OB = OA + AP + BP .........................(2)
we know that,
AP = AC = r = radius of smaller circle,&,
BP = BD = R = radius of bigger circle,
NOW,
\frac{1}{\sin 30^\circ} = \frac {OB}{BD}
\Rightarrow 2 = \frac {OA + AP + R}{R}
\Rightarrow 2*R = 30+15+R..................(from.......(1)),
\Rightarrow 2R - R = 45
\Rightarrow R = 45
so, putting values of R , OA , AP in equation (2),
we get, OB = 30+15 + 45 = 90........................Answer.
Join OB, it passes through A. Draw 2 radii from A to the point of contact of the tangent to the smaller circle. Name these points L and M. Δ O A L ≅ Δ O A M Because O A = O A [ common side ] , ∠ O L A = ∠ O M A = 9 0 ∘ and
O L = O M [ tangent from same point are equal in length ]
Therefore ∠ L O A = ∠ M O A = 3 0 ∘ [ C.P.C.T ]
Since A L = 1 5 , ⇒ A O = 3 0
Further, distance from point of contact of the circle (say C) and A = 15 (radius)
Therefore AC=45
Let, radius of larger circle be x . Draw a radius from B to point of contact of the tangent. (say D). B D = x and O B = 4 5 + x
In right triangle Δ B O D we have 4 5 + x x = sin 3 0 ∘
or, 4 5 + x x = 2 1 which on solving gives x = 4 5
Hence our answer for O B = 4 5 + x = 4 5 + 4 5 = 9 0 . Cheers.
Join A to O. Let OA = x cm . Let C & D be the tangent points of the smaller circle with the line then by property of tangents we have AD & AC perpendicular to the two tangents respectively. We can prove that triangles ACO and ADO are congruent thus OA is the angle bisector of the angle made by the two lines. In triangle ADC , we have AD/AO = sin 30 = 15/x x= 30 SImilarly in the larger triangle made
OA=2 R_A =2 15=30 OA+R A+R B= OB= 2 R_B --> 45+R_B=2 R B --> R B=45 & OB=90
create an equilateral triangle OCD where the small circle is its incircle. We see that the bigger circle is the excircle.
ratio of radius of the incircle to radius of the excircle of an equilateral triangle is 3 1 .
so, radius of the bigger circle is:
R = 3 r = 4 5
O B R = sin 3 0 ∘ O B 4 5 = 2 1 O B = 9 0
Let the lines be O C D and O C ′ D ′ , where C and C ′ are the points of tangency from O to the smaller circle and D and D ′ are the points of tangency from O to the larger circle. Thus, we have ∠ O C A = ∠ O C ′ A = ∠ O D B = ∠ O D ′ B = 9 0 ∘ and by symmetry we have that ∠ A O C = ∠ A O C ′ = ∠ B O D = ∠ B O D ′ = 2 6 0 ∘ = 3 0 ∘ . Hence O A B is a straight line.
Let r be the radius of the larger circle. We notice that O A C and O B D are 3 0 ∘ − 6 0 ∘ − 9 0 ∘ triangles, thus O A = 2 A C = 2 ⋅ 1 5 = 3 0 and O B = 2 B D = 2 r . We also have that O B = O A + 1 5 + r = 4 5 + r . Thus the radius of the largest circle is 2 r = 4 5 + r ⇒ r = 4 5 . Hence O B = 2 r = 9 0 .
In this case a 30°×60° triangle is formed having
base=1, height =√3 and hyp.= 2.
By similar triangles,
OA / 15 = OB /R, where R= radius of the big circle
OA=2×15= 30 and OC= 30+15+R = 45R
30/15 = 45+R / R
30R= 15R+ 675
R = 45
And OB= 45+ 45 = 90 cms.
Drop a line from A to point C on one of the lines forming angle O, perpendicular to it. AC/OA=0.5 ( sin 30deg.) thus OA =30. By similarity, OB is double the distance from circumference of circle B To O, or 2*(30+15)
Assume :
Radius of the smaller circle = rA
Radius of the larger circle = rB
Then,
sin 60 = 15 / OA
OA = 15 / sin 60 = 30
sin 60 = rB / (30 + 15 + rB)
1 / 2 = rB / (45 + rB)
45 + rB = 2 rB
rB = 45
Hence,
OB = 30 + 15 + 45 = 90
Let us denote point of the tangent of circle A as A ′ .
Let us denote point of the tangent of circle B as B ′ .
Let us denote radius of circle B as x and the intersection of circle A and B as C .
Note that, ∠ O A ′ A = 9 0 ∘ and ∠ O B ′ B = 9 0 ∘ .
As O, A, and B are collinear, ∠ B O B ′ = ∠ A O A ′ = 6 0 ∘ / 2 = 3 0 ∘ .
A A ′ = radius of circle A = 15.
sin ∠ A O A ′ = O A A A ′
sin 3 0 ∘ = O A 1 5 --> O A = 1 5 ∗ 2 = 3 0 .
Hence, the equation of sin ∠ B O B ′ = O B B B ′ also holds.
sin 3 0 ∘ = O A + A C + C B B B ′
2 1 = 3 0 + 1 5 + x x
2 1 = 4 5 + x x
4 5 + x = 2 x --> Hence x = 4 5
Thus, the length of OB is defined by O A + A C + C B = 3 0 + 1 5 + 4 5 = 9 0 .