This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
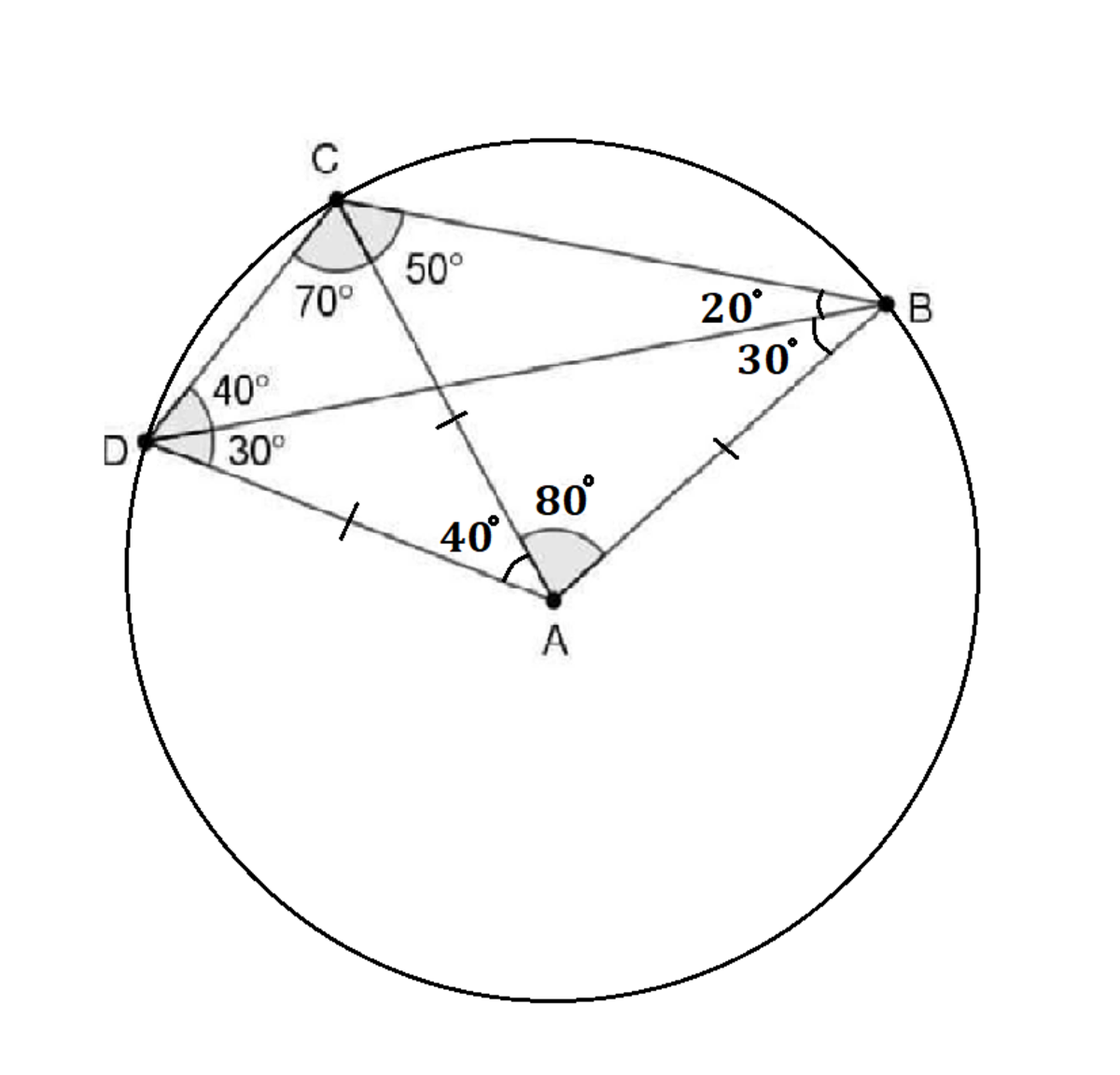
What is the motivation for inscribing the figure in a circle?
Log in to reply
@Elijah L angle DAC is 40 deg .. which we can figure out from the given angles in triangle ACD.. also ACD is an Iso triangle with AC=AD, again angle DBC is 20 deg .. which is half of angle DAC.. both of these conditions supports the property of a circle (subtending angles arc and centre.. ) again reflex angle DCB = 240... and angle DAB = 120.. as we can cross check... so all these points 'D' 'C' & 'B' lie on the circumference of a circle...
∣ C D ∣ = 2 ∣ A D ∣ sin 2 0 ° .
In △ B C D , sin 2 0 ° ∣ C D ∣ = sin 1 2 0 ° ∣ B D ∣
⟹ ∣ B D ∣ = 3 ∣ A D ∣ .
In △ A B D , sin ( 1 1 0 ° − x ) ∣ A D ∣ = sin ( 4 0 ° + x ) ∣ B D ∣
⟹ tan x = cos 4 0 ° − 3 sin 2 0 ° 3 cos 2 0 ° − sin 4 0 °
= cos 2 0 ° − 3 sin 2 0 ° sin 2 0 ° + 3 cos 2 0 °
= cos ( 2 0 ° + tan − 1 3 ) cos ( 2 0 ° − tan − 1 3 1 )
= cos 8 0 ° cos 1 0 ° = tan 8 0 °
⟹ x = 8 0 ° .
Nice solution from @Nibedan Mukherjee . To show that the solution works, we have to show that A B = A C = A D . Then A is the center of a circle of radius A B and △ A B D is isosceles, and x = 1 8 0 ∘ − 2 ( 3 0 ∘ ) − 4 0 ∘ = 8 0 ∘ . Let A B = A C = A D = 1 . We need to show A B = 1 .
Since △ A C D is isosceles, A C = A D = 1 . Then C D = 2 sin 2 0 ∘ . Let the diagonals of A B C D intersect at E . We note that △ C D E is isosceles and C E = 4 sin 2 2 0 ∘ . Then A E = A C − C E = 1 − 4 sin 2 2 0 ∘ = 2 cos 4 0 c i r c − 1 .
By sine rule , sin 5 0 ∘ B E = sin 2 0 ∘ C E ⟹ B E = 4 sin 2 0 ∘ sin 5 0 ∘ = 4 sin 2 0 ∘ cos 4 0 ∘ .
By cosine rule ,
A B 2 ⟹ A B = A E 2 + B E 2 − 2 A E ⋅ B E cos ∠ A E B = ( 2 cos 4 0 ∘ − 1 ) 2 + ( 4 sin 2 0 ∘ cos 4 0 ∘ ) 2 − 8 ( 2 cos 4 0 ∘ − 1 ) sin 2 0 ∘ cos 4 0 ∘ cos 7 0 ∘ As cos 7 0 ∘ = sin 2 0 ∘ = 4 cos 2 4 0 ∘ − 4 cos 4 0 ∘ + 1 + 1 6 sin 2 2 0 ∘ cos 2 4 0 ∘ − 1 6 sin 2 2 0 ∘ cos 2 4 0 ∘ + 8 sin 2 2 0 ∘ cos 4 0 ∘ = 4 cos 2 4 0 ∘ + 1 − 4 cos 4 0 ∘ ( 1 − 2 sin 2 2 0 ∘ ) = 4 cos 2 4 0 ∘ + 1 − 4 cos 2 4 0 ∘ = 1 = 1
You need to remove the part "Let A B = 1 " in your initial statement.