Nine Circles
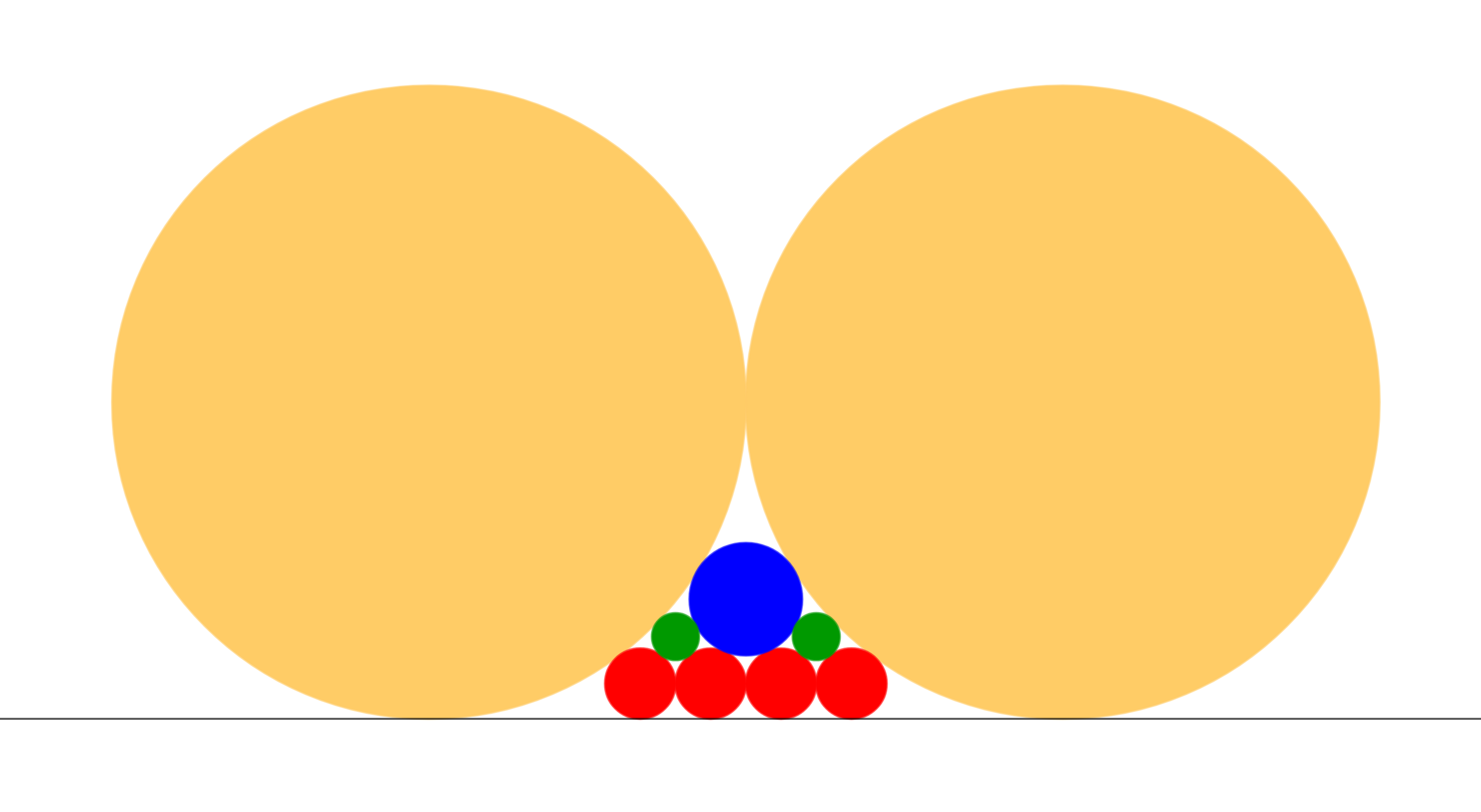
The figure shows nine externally tangent circles. The yellow and red circles are also tangent to a line. Congruent circles are colored alike. If the radius of the green circle is 10, what is the radius of the large yellow circle?
The answer is 135.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the system is symmetrical about the center line, let us consider half of the circles on the right. Let the radius of red circle be r and the radius of the large yellow circle be R . Consider the line A E whose length is R . Then
A D + D E A D + D G 2 − G E 2 3 r + ( R + r ) 2 − ( R − r ) 2 3 r + 2 r R − R ( 3 r − R ) ( r + R ) 3 r ⟹ R = A E = A E = R = 0 = 0 = R = 9 r Since R > r > 0
Also
A C + C E A C + F H A C + F G 2 − G H 2 A C + F G 2 − ( G I − H E − E I ) 2 2 r + ( R + 1 0 ) 2 − ( R − F C − r ) 2 2 r + ( 9 r + 1 0 ) 2 − ( 8 r − ( r + 1 0 ) 2 − r 2 ) 2 ( 9 r + 1 0 ) 2 − ( 8 r − 2 0 r + 1 0 0 ) 2 8 1 r 2 + 1 8 0 r + 1 0 0 − ( 6 4 r 2 − 1 6 r 2 0 r + 1 0 0 + 2 0 r + 1 0 0 ) 1 6 r 2 0 r + 1 0 0 5 r + 2 5 5 r + 2 5 ⟹ r R = A E = A E = A E = A E = R = 9 r = 7 r = 4 9 r 2 = 3 2 r 2 − 1 6 0 r = r − 5 = r 2 − 1 0 r + 2 5 = 1 5 = 9 r = 1 3 5 Since r > 0 Squaring both sides.