NMTC 2014(Junior level)
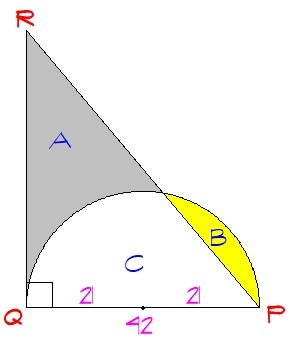
 In the given figure,
P
Q
=
4
2
cm
.
Q
R
is the tangent to the semicircle at
Q
. If the difference of the areas of region
A
and
B
is
3
5
7
cm
2
, then the base
Q
R
of the right triangle
P
Q
R
is (in cm)(Take
π
=
7
2
2
)
In the given figure,
P
Q
=
4
2
cm
.
Q
R
is the tangent to the semicircle at
Q
. If the difference of the areas of region
A
and
B
is
3
5
7
cm
2
, then the base
Q
R
of the right triangle
P
Q
R
is (in cm)(Take
π
=
7
2
2
)
Note: This problem has appeared in nmtc 2014 junior level.
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Did the Exact same
 Let
T
be the area of
△
R
Q
P
and
C
be the area of the unshaded region of the semicircle.
Let
T
be the area of
△
R
Q
P
and
C
be the area of the unshaded region of the semicircle.
T = 2 1 ( R Q ) ( 4 2 ) = 2 1 R Q ( 1 )
A = T − C ( 2 )
C = 2 1 π ( 2 1 2 ) − B = 2 1 ( 7 2 2 ) ( 4 4 1 ) − B = 6 9 3 − B ( 3 )
Substitute ( 1 ) and ( 3 ) in ( 2 ) .
A = 2 1 R Q − ( 6 9 3 − B ) = 2 1 R Q − 6 9 3 + B
A − B + 6 9 3 = 2 1 R Q
3 5 7 + 6 9 3 = 2 1 R Q
1 0 5 0 = 2 1 R Q
5 0 = R Q
The area of triangle P Q R is A plus the semicircle minus B . Since A − B = 3 5 7 , then the area of P Q R is the area of the semicircle plus 3 5 7 . The area of the semicircle is 2 2 1 2 π = 2 4 4 1 π
Let Q R = x . Then the area of P Q R is also equal to 2 4 2 x = 2 1 x . We can set the two areas equal to get the equation 2 4 4 1 π + 3 5 7 = 2 1 x Dividing both sides by 21 gives us 2 2 1 π + 1 7 = x Since π = 7 2 2 , then x = 2 2 1 × 7 2 2 + 7 = 3 × 1 1 + 1 7 = 5 0
Let non-shaded area of the semicircle be C . Therefore, the area of the semicircle − C = B and if the radius of the semicircle is r = 2 1 .
⇒ 2 1 π r 2 − C = B . . . ( 1 )
We also note that, the area of △ P Q R − C = A and if Q R = h , then:
⇒ 2 1 ( 2 r ) h − C = A ⇒ r h − C = A . . . ( 2 )
Equation 2 - Equation 1:
⇒ r h − 2 1 π r 2 = A − B = 3 5 7 ⇒ h = r 3 5 7 + 2 π r ⇒ h = 2 1 3 5 7 + 7 2 2 × 2 2 1 = 1 7 + 3 3 = 5 0