NMTC 2K15 #29 Kaprekar Contest
is a rectangle. and . is the arc of the circle centered . Find the length of .
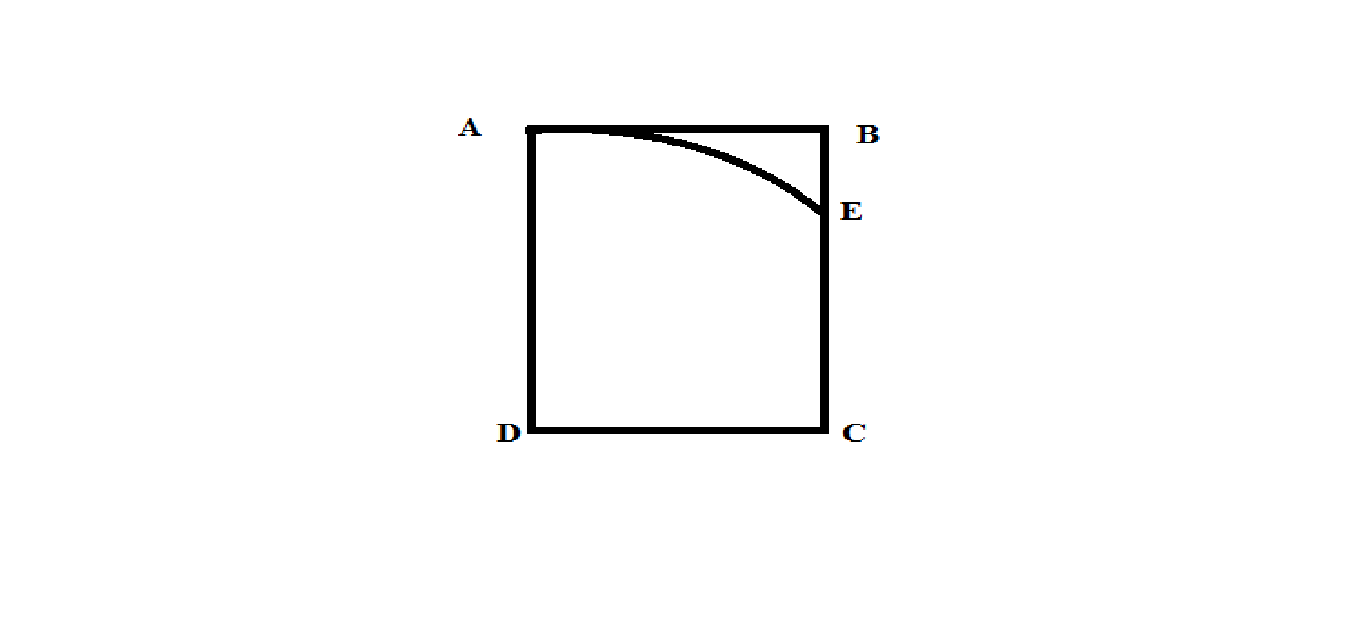
Note: Give your answer to 3 decimal places.
The answer is 0.268.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A E is the arc of the circle centered D
⇒ A D is the radius of the circle.
Now, we know that the distance from the centre of the circle to the boundary is always uniform. Hence,
⇒ D E = A D = radius of the circle = 2
Now,see the figure.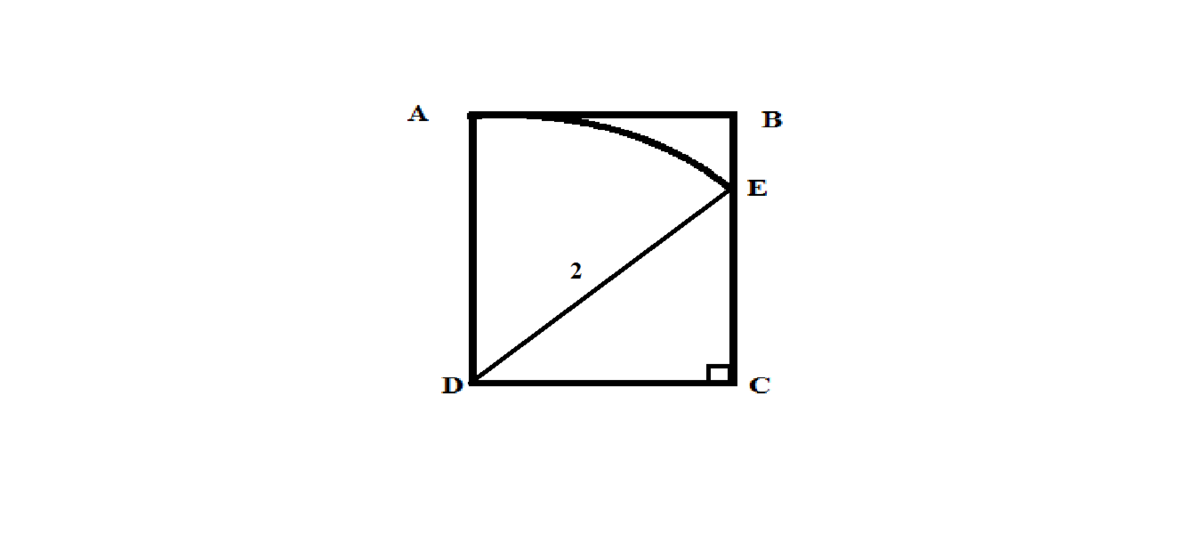 ⇒
△
D
E
C
is right-angled at
C
.
⇒
△
D
E
C
is right-angled at
C
.
Now, according to pythogorean theorem,
⇒ ( D E ) 2 = ( E C ) 2 + ( D C ) 2
⇒ 4 = ( E C ) 2 + 1
⇒ E C = 3
∴ B E = B C − E C = 2 − 3
∴ B E = 0 . 2 6 8