$n^n$ Congruence

Computer Science Level 4

$\large { n }^{ n }\equiv n \pmod{100}$

How many positive integers $n$ less than 100 satisfy the above congruence?

The answer is 21.

5 solutions

Arjen Vreugdenhil
Mar 24, 2016

There is no need to calculate big numbers like $n^n$ . After each multiplication we can reduce the product modulo 100. This will keep everything well within usual integer range (and faster!)

int c = 0;

for (int n = 1; n < 100; n++) {
    int p = 1;
    for (int i = 1; i <= n; i++) {
        p *= n; p %= 100;
    }
    if (p == n) {
        System.out.print(n);
        System.out.print("  "); 
        c++;
    }
}

System.out.println();
System.out.println(c);

Output:

1 2	`1 11 16 21 25 31 36 41 49 51 56 57 61 71 75 76 81 91 93 96 99 21`

It depends, eh. (Some youngster caught me making an assertion like this a few months ago.) Here is a pair of Python codes and their timings.

import time

repetitions=10000

start_time=time.time()
for r in range(repetitions):
    count=0
    for n in range(1,100):
        count+=n==(n**n)%100
end_time=time.time()
print (end_time-start_time)
print (count)

start_time=time.time()
for r in range(repetitions):
    count=0
    for n in range(1,100):
        prod=n
        for i in range(1,n):
            prod*=n
            prod%=100
        count+=prod==n
end_time=time.time()
print (end_time-start_time)
print (count)

Output:

>pythonw -u "temp.py"
2.783202886581421
21
31.87304711341858
21
>Exit code: 0

Bill Bell - 5 years, 1 month ago

Did exactly the same (+1)!

Samarth Agarwal - 5 years, 2 months ago

Eugene Lee
Mar 19, 2016

I used Python to do this question. Code below:

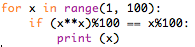
Note: Using pow(a,d,n) is faster than using (a**d)%n and both give the same result.

When you don't need to explicitly evaluate the exponentiated value but just need to do modular exponentiation, use the pow() function with 3 parameters.

Prasun Biswas - 5 years, 2 months ago

Similar here. But I use x instead of x%100, because x is less than 100.

展豪張 - 5 years, 2 months ago

Python one-liner:

1 2	`>>> len([n for n in xrange(1,100) if pow(n,n,100)==n]) 21`

Laurent Shorts - 5 years, 2 months ago

the same...but level 4 is to much for this

Omar El Mokhtar - 5 years, 1 month ago

Khang Nguyen Thanh
Mar 24, 2016

I used C++ to solve.

#include <iostream>
using namespace std;

int modpow(int a, int b, int n) {
     int rs = 1;
     while (b > 0) {
           if ((b % 2) == 1) {
                  rs = (rs * a) % n;
                  --b;
           }
           b /= 2;
           a = (a * a) % n;
    } 
    return rs;
}

int main() {
    int count = 0;
    for (int n = 1; n < 100; n++) {
        int mod = modpow(n, n, 100);
        if (mod == n) count++;
    }
    cout << count;
    return 0;
}

The output is 21 .

David Holcer
Mar 27, 2016

count=0
for n in range (1,101):
    if pow(n,n,100)==n: count+=1
print count

quicky. Implemented pow(x,y,z) thanks to @Prasun Biswas who commented it was faster.

Kushagra Sahni
Mar 18, 2016

For numbers ending in 1 we can have n=1,11,21,.....91 ie all 10.
For 3 we have only 93.
For 5 we have 25 and 75.
For 6 we have 16,36,56,76,96.
For 7 we have only 57.
For 9 we have 49,99.
No solutions for 2,4,8.
So we have 23 numbers in all

How did you arrive at these numbers?

Vishnu Bhagyanath - 5 years, 2 months ago

The proof is a bit long. I basically proved that n^n-n in these cases is divisible by 100.

Kushagra Sahni - 5 years, 2 months ago

Post that, that is what is required as a solution, not just the answer.

Vishnu Bhagyanath - 5 years, 2 months ago

n n n^n n n Congruence

The answer is 21.

5 solutions

0 pending reports

$n^n$ Congruence