No 0's at all!
A and B are whole numbers that do not contain 0 as a digit when expressed in base 10
If A × B = 1 0 0 0 0 , then what is A + B ?
The answer is 641.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
nice solution..
We are kind of lucky in this problem that 2^4 and 5^4 have no zeros.
Log in to reply
Good point. 2^9 and 5^8 each have zeros. So was it luck that this problem didn’t involve 10^9 or 10^8? Or careful design?
Maybe I don't know enough math or English te understand the question completely but I had this interpretation. Writing 10000 as the product of 2 whole numbers that as a 10 base have no zeroes in the digits leads to 250 x 40 which as 10 base is (25x10^1) x (4x10^1) which satisfies the condition. The sum of these numbers is 290.clearly the wrong answer. Where is my interpretation wrong?
Log in to reply
The expressions 25x10^1 and 8x10^1 are written in scientific notation, not base ten — or 10 base, as you call it — notation.
The numbers 250 and 80 are written in base ten notation. Contrary to a condition of the problem, 0 does appear as a digit — in the ones place in each number.
؟؟؟؟؟؟؟؟؟؟؟؟؟؟
Without writing down, this is pretty much random guess from well known factors
10,000 should = xx5 * xx2
And, it's known that 125 * 8 = 1,000 => 10,000 = 125 * 80. To eliminate zero from 80, divide it by something odd, like 5: 80 / 5 = 16. Next: 125 * 5 = 625
=> 10,000 = 16 * 625
-- Edited: Just read other comments, I think prime factorization is the formal academic solution to this.
But I like your solution (Y)
I’m taken with your “guess and check (and adjust)” procedure of arriving at the 5^4 * 2^4 solution. Fun to follow.
But I’m curious about the meaning of xx5 * xx2 and how 125 * 8 comes from that. (Is it 5 5 5 and 2 2 2? IOW 5^3 and 2^3?) Interesting how close to the final solution you were early on.
Neat solution.
just refer to Fox' theorem
Haven’t heard of Fox theorem. What is it?
I don’t know either
10000 = 100x100= 25x4x25×4 = 625*16. Hence the required sum is 625+16 = 641
A×B=100×100=(4×25)×(4×25)=16×625,A+B=641##
It can be easily solved by prime factorization method. Prime factors of 10000 can be written as
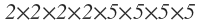 Now separate the terms which do not contain 0 as digit. The only way to do this is to keep all 2s and 5s separate i.e.
Now separate the terms which do not contain 0 as digit. The only way to do this is to keep all 2s and 5s separate i.e.
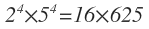 And hence,
And hence,
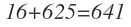
10000=2^4*5^4=10^4 2^4=16 5^4=625 16+625=641. Both 625 and 16 have no 0s.
At first glance, we all think that 10000 is 10x10x10x10(correct), but the secret here is that 10=2x5
So 10000 =10x10x10x10=2x2x2x2x5x5x5x5=2^4 x 5^4.
2^4=16
5^4=625
625+16=641
I know these sums are messy. Sorry!
Use latex. It’s really nice. Before i used latex, my solutions looked like chicken scratch. And they still do now.
Log in to reply
Oh. Ok. Thanks.
Then, why do you say to him, "Use Latex"?
Expressed as a product of its prime factors, 1 0 0 0 0 = 2 4 ⋅ 5 4
A = 2 4 = 1 6
B = 5 4 = 6 2 5
∴ A + B = 1 6 + 6 2 5 = 6 4 1
625 x 16 = 10000, 625 + 16 = 641
Factors 10000 are four 2's and four 5's. We get a zero only when we multiply 2&5 . so answer would be 5^4+2^4
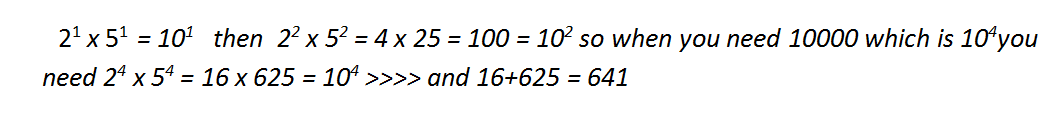
Note that 1 0 0 0 0 = 1 0 4 = 2 4 ⋅ 5 4 . Any number which has 2 AND 5 as factors will end in a 0, so the only possible way to write 10000 as a product of two numbers which don't contain 0s is 1 0 0 0 0 = 2 4 ⋅ 5 4 = 1 6 ⋅ 6 2 5 , so the sum is 1 6 + 6 2 5 = 6 4 1 .