No 1874 Sangaku Problem
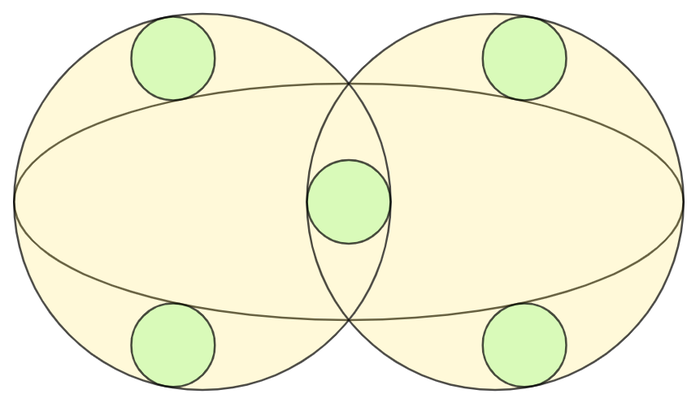
Two large circles altogether inscribe five identical small circles (in green) and an ellipse, which are each centrally and symmetrically positioned as shown above. One of the five small circles has one point of tangency with each of the large circle, whereas four others have one point of tangency with their respective large circle and one point of tangency with the ellipse.
If the eccentricity of an ellipse is , input as your answer.
The answer is 935414.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Place the whole diagram so that its center is at the origin and the two large circles are unit circles with centers at ( ± k , 0 ) .
Then the two large circles have equations of ( x ± k ) 2 + y 2 = 1 , which intersect at ( 0 , ± 1 − k 2 ) .
The semi-major axis of the ellipse is a = k + 1 , the semi-minor axis of the ellipse is b = 1 − k 2 , and the radius of one green circle is r = 1 − k .
Then the ellipse has an equation of ( k + 1 ) 2 x 2 + 1 − k 2 y 2 = 1 .
The three left-most green circles are tangent to a circle also centered at ( k , 0 ) but with a radius of R = 1 − 2 r = 1 − 2 ( 1 − k ) = 2 k − 1 , so an equation of ( x − k ) 2 + y 2 = ( 2 k − 1 ) 2 , and this circle must also be tangent to the ellipse.
Substituting ( x − k ) 2 + y 2 = ( 2 k − 1 ) 2 into ( k + 1 ) 2 x 2 + 1 − k 2 y 2 = 1 gives ( k + 1 ) 2 x 2 + 1 − k 2 ( 2 k − 1 ) 2 − ( x − k ) 2 = 1 , and for that circle to be tangent to the ellipse its discriminant 9 k 2 + 2 k − 7 must equal 0 , and 9 k 2 + 2 k − 7 = 0 solves to k = 9 7 .
That makes the semi-major axis a = k + 1 = 9 7 + 1 = 9 1 6 and the semi-minor axis b = 1 − k 2 = 1 − ( 9 7 ) 2 = 9 4 2 , for an eccentricity of e = a a 2 − b 2 = 9 1 6 ( 9 1 6 ) 2 − ( 9 4 2 ) 2 = 4 1 4 ≈ 0 . 9 3 5 4 1 4 3 , so ⌊ 1 0 6 e ⌋ = 9 3 5 4 1 4 .