No AM-GM here!
∫ 0 2 π a 2 sin 2 x + 9 cos 2 x d x
Over all constant real values of a , what is the minimial value of the above expression?
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
This can be transformed into an ellipse equation. The integral refers to total length of ellipse The minimal length happens when a=0. Length of ellipse becomes 2*(2 * 3)=12
Differentiate the above equation w.r.t. to ′ a ′ . And then using integral under the derivative we see it is minimum at a = 0 .
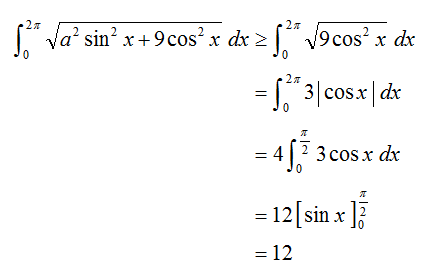
We have:
∫ 0 2 π a 2 sin 2 x + 9 cos 2 x d x ≥ ∫ 0 2 π 9 cos 2 x d x = ∫ 0 2 π 3 ∣ cos x ∣ d x = 3 ∫ 0 2 π cos x d x − 3 ∫ 2 π 2 3 π cos x d x + 3 ∫ 2 3 π 2 π cos x d x = 1 2