No angle allowed!
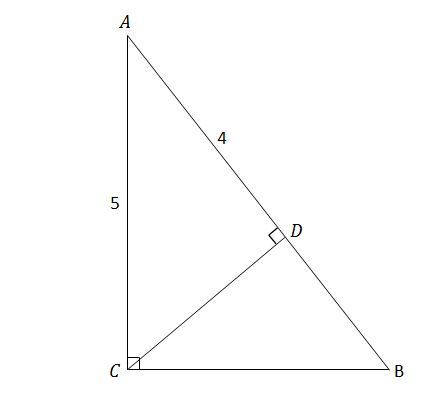 Triangle
A
B
C
is a right triangle with a side length
∣
∣
A
C
∣
∣
=
5
,
∠
C
=
9
0
∘
and the measures of
∠
A
and
∠
B
unknown. If
D
is a point on
A
B
such that
∠
A
D
C
=
9
0
∘
and
∣
∣
A
D
∣
∣
=
4
,
what is
∣
∣
B
C
∣
∣
?
Triangle
A
B
C
is a right triangle with a side length
∣
∣
A
C
∣
∣
=
5
,
∠
C
=
9
0
∘
and the measures of
∠
A
and
∠
B
unknown. If
D
is a point on
A
B
such that
∠
A
D
C
=
9
0
∘
and
∣
∣
A
D
∣
∣
=
4
,
what is
∣
∣
B
C
∣
∣
?
The answer is 3.75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
This is more clear solution.
We could determine that CD = 3 through Pythagorean Triplets.
Then if we draw an arc with radius equal to 5, we could determine that BC is a tangent and is equal to 5 tan A . So BC is:
B C = 5 tan A = 5 ( 4 3 ) B C = 3 . 7 5
∠ B A C = ∠ C A D and ∠ A C B = ∠ A D C = 9 0 ° leaving ∠ A B C = ∠ A C D .
This makes ABC and ACD similar triangles so we can just compare ratios.
CD is 3/4th of AD, since it is 3 (per the most famous example of Pythagorean Theorem) and 3 = 0 . 7 5 ∗ 4 .
BC is 3/4th of AC, making it 3.75 because 3 . 7 5 = 0 . 7 5 ∗ 5 .
Take triangle A D C
A C 2 = A D 2 + D C 2
5 2 = 4 2 + D C 2
2 5 − 1 6 = D C 2
3 = D C
Take D B as x .
In triangle A B C ;
5 2 + B C 2 = ( 4 + x ) 2
1 6 + x 2 + 8 x − 2 5 = B C 2 ( 1 )
In triangle B C D
D C 2 + B D 2 = B C 2
3 2 + x 2 = B C 2 ( 2 )
Equating 1 & 2
1 6 + x 2 + 8 x − 2 5 = B C 2 = 3 2 + x 2 = B C 2
8 x = 1 8
x = 2 . 2 5
Therefore; A B = 4 + 2 . 2 5 = 6 . 2 5
By Pythagoras Theorem; 6.25^{2} - 5^{2) = BC^2
3 9 . 0 6 2 5 − 2 5 = B C 2
1 4 . 0 6 2 5 = B C 2
B C = 3 . 7 5