No calculus required!
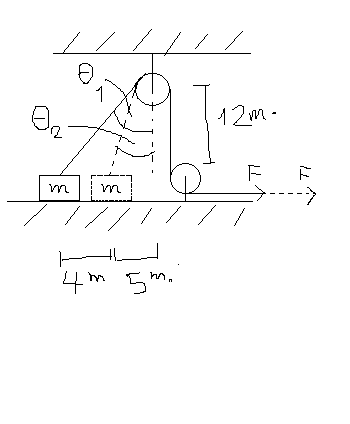 From the figure (sorry for "paint" quality XD). A mass
is placed on a frictionless surface with angle
to the vertical line. It's pulled by constant force
using a massless string such that the mass don't float when it's pulled. After I stop pulling this mass when the rope does the angle
to the vertical line, find the amount of work done by
in
at the point when I stop pulling it.
From the figure (sorry for "paint" quality XD). A mass
is placed on a frictionless surface with angle
to the vertical line. It's pulled by constant force
using a massless string such that the mass don't float when it's pulled. After I stop pulling this mass when the rope does the angle
to the vertical line, find the amount of work done by
in
at the point when I stop pulling it.
Details:
- Pulleys are very strong that they always stay still, massless, and frictionless.
- This problem is from my physics teacher.
The answer is 84.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
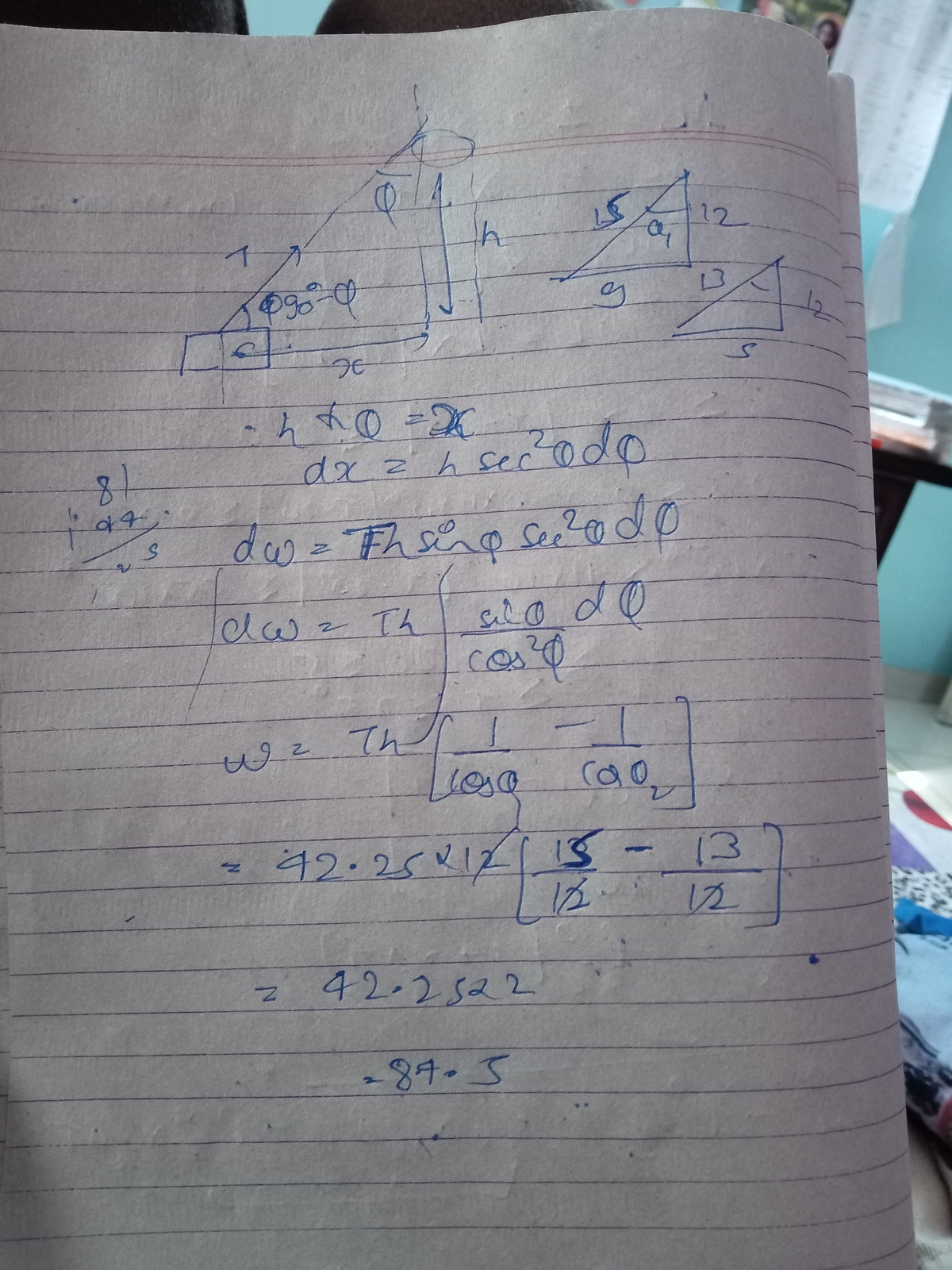
The work done is F* the parallel component of the displacement. The parallel component of the displacement can be found by finding the change in the length of the string from theta 1 to theta 2, because that's how much string the force F pulls. Thus delta x = sqrt(12^2+9^2) - sqrt(12^2+5^2) = 2m. Work = 2*42.25 = 84.5 Joules