No hope to reach the center
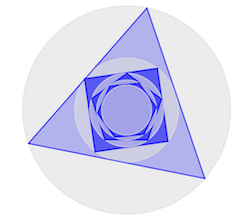 The image shows a sequence of inscribed regular polygons and circles. Each step, the number of sides of the polygon is increased by 1. Let
be the radius of the innermost circle after
steps and
, the radius of the largest circle.
The image shows a sequence of inscribed regular polygons and circles. Each step, the number of sides of the polygon is increased by 1. Let
be the radius of the innermost circle after
steps and
, the radius of the largest circle.
Find
The answer is 0.114942.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Applying the recurrence from the start, with r 0 = 1 , we get:
r ∞ = N = 3 ∏ ∞ cos ( N π ) ≈ 0 . 1 1 4 9 4 2
I evaluated the infinite product using Wolfram Alpha .