No Integration Necessary (Part 2)
2 5 x 2 + 4 y 2 = 1
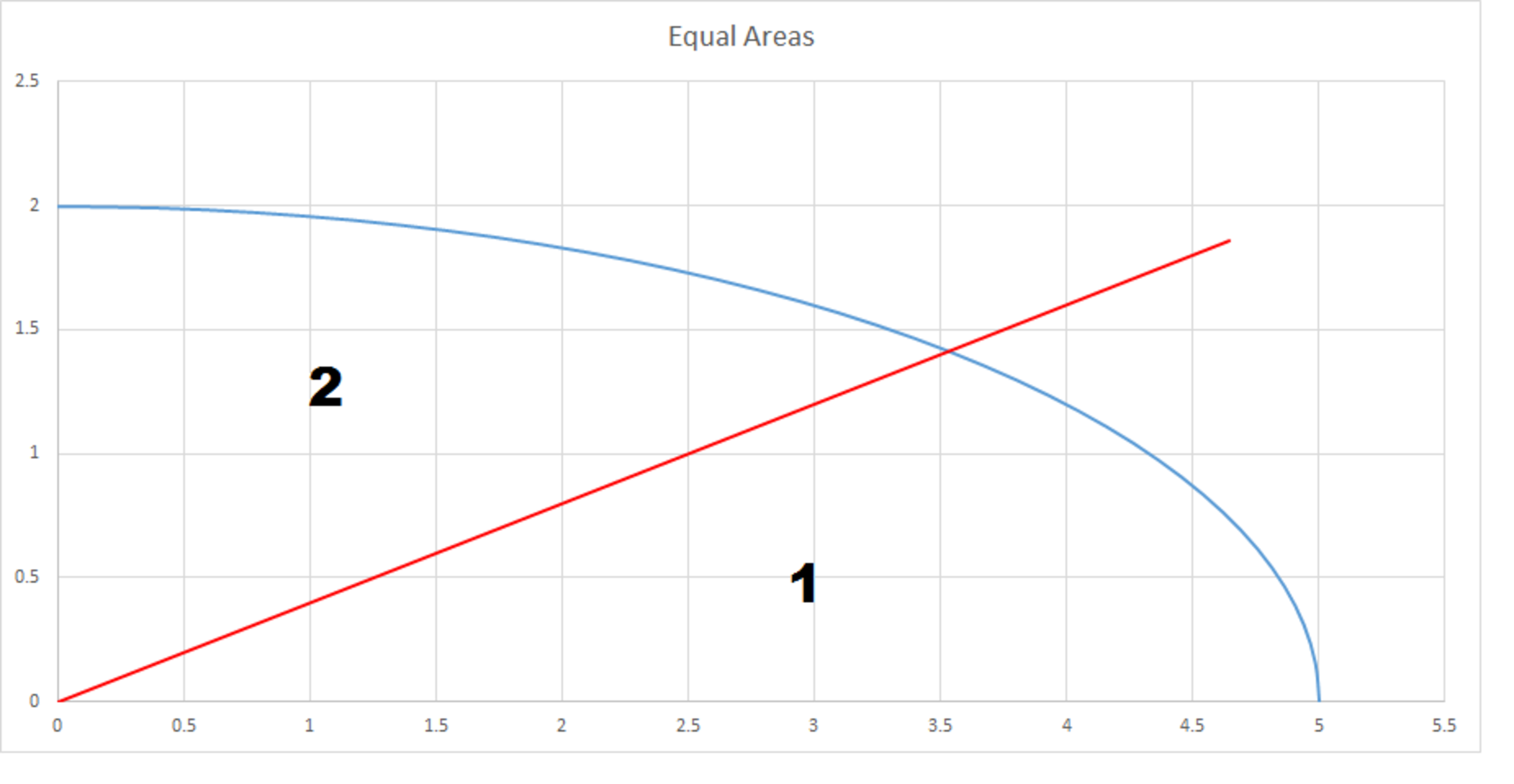
The figure above depicts the portion of the ellipse whose equation is given above, which lies in the first quadrant.
Find the acute angle (in degrees) that a line passing through the origin makes with the x -axis, such that the line divides the quarter-ellipse into two segments with equal areas.
Give your answer to 1 decimal place.
The answer is 21.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Okay, I went against the recommendation given in the question because I simply love calculus. For the given ellipse, the semi-major axis is a = 5 and the semi-minor axis is b = 2 Let the equation of the line be y = m x since it passes through the origin. Solving this and the equation for the ellipse for x gives you the x coordinate of the intersection point of the line and the ellipse. x = 2 5 m 2 + 4 1 0 = k Now, the line cuts the quarter ellipse into two halves of equal area. Since the area under the quarter ellipse is 4 π a b , each of the area cut by the line is 8 π a b o r 4 5 π Now solve the equation ∫ 0 k m x d x + ∫ k 5 5 2 2 5 − x 2 d x = 4 5 π Do this, substitute for k and get the equation: 2 π − sin − 1 2 5 m 2 + 4 2 = 4 π or, cos − 1 2 5 m 2 + 4 2 = 4 π or, tan − 1 2 5 m = 4 π or, 2 5 m = 1 or, m = 5 2 Finally, the angle made by the line with the x-axis is tan − 1 m = tan − 1 5 2 = 0 . 3 8 r a d = 2 1 . 8 ∘ .
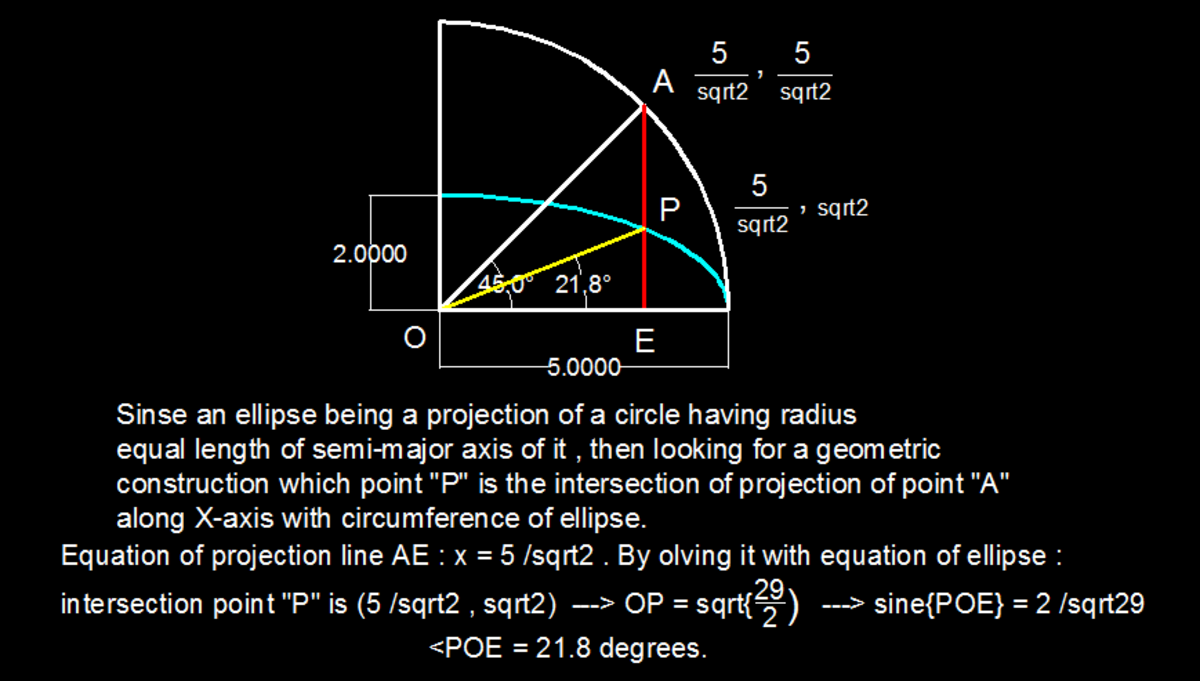
Consider the circle circumscribing the ellipse. It will have a radius = semi major axis = 5 This circle is 'tilted' about the x axis to get the given ellipse. The tilt is such that the vertical radius 5 is now seen as 2 units. So a line with 45° inclination dividing the quarter circle in two equal areas will now have an inclination arctan 5 2 = 2 1 . 8 0