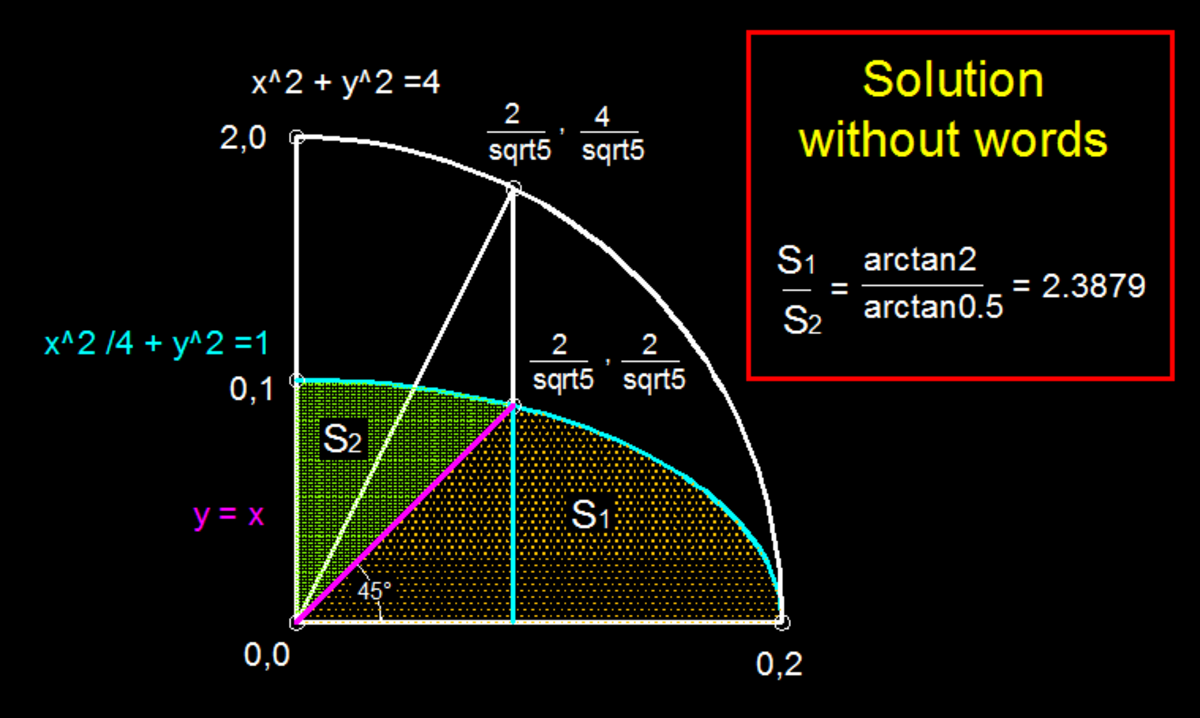
No Integration Necessary

Geometry Level 5

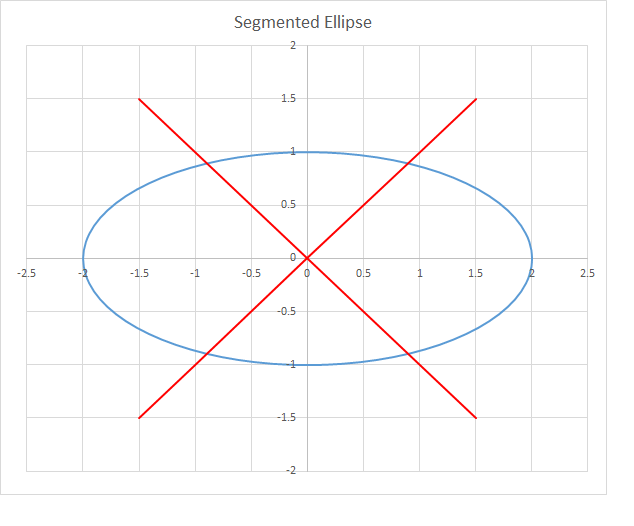
The figure above shows the graph of an ellipse having a horizontal semi-major axis of 2 units, and a vertical semi-minor axis of 1 unit. That is, its equation is

x 2 4 + y 2 = 1 \frac{x^2}{4} + y^2 = 1

Two perpendicular lines (shown in red) are at 45 degrees with the x x -axis, and pass through the origin. They segment the ellipse into 4 segments. From symmetry, there are only two distinct values of the area of a segment. Find the ratio of the area of the larger segment to the area of the smaller segment.


The answer is 2.388.

Hosam Hajjir by Hosam Hajjir , 56, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Ahmad Saad
Jul 15, 2016

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Atomsky Jahid
Jul 13, 2016

You can easily integrate and find the result. The integration requires trigonometric substitution only.

But, there's another way to solve it. We'll look for axis transformation which will change our ellipse into a circle.

Let, X = x 2 X=\frac{x}{2} Then, our ellipse is an circle in X − y X-y axes. And, the lines y = ± x y=\pm x change to y = ± 2 X y=\pm 2X . Now, you can find the angle which the line y = 2 X y=2X makes with X-axis. Therefore, the first quadrant is divided into t a n − 1 2 tan^{-1}2 and t a n − 1 1 2 tan^{-1}\frac{1}{2} . These angles are proportional to the divided area. So, the required ratio is t a n − 1 2 t a n − 1 0.5 ≈ 2.388 \frac{tan^{-1}2}{tan^{-1}0.5} \approx \boxed{2.388}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...