No, its impossible

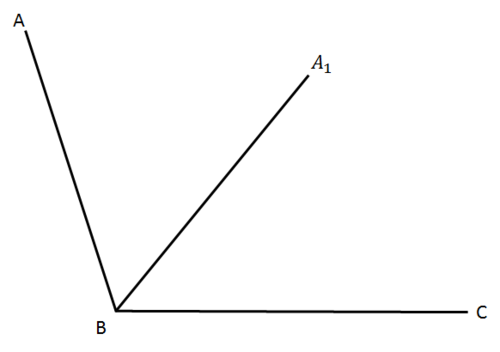Suppose I have $\angle ABC$ , and I draw out an angle bisector of $\angle ABC$ , such that $\angle ABA_{1} = \angle CBA_{1}$ as described above.

Next, I make an angle bisector of $\angle CBA_{1}$ , such that $\angle A_{1}BA_{2} = \angle A_{2} BC$

Next, I make an angle bisector of $\angle A_{1}BA_{2}$ , such that $\angle A_{1}BA_{3} = \angle A_{3}BA_{2}$

Next, I make an angle bisector of $\angle A_{3}BA_{2}$ , such that $\angle A_{3}BA_{4} = \angle A_{4}BA_{2}$

If I am to repeat this algorithm forever, find $\lim _{ n\rightarrow \infty }{ \frac { \angle { A }_{ n }BC }{ \angle { A }BC } }$

Give your answer to 3 decimal places.