No Measures Given
Let △ A B C be a triangle with A B > B C , right angled at B and inscribed in the circle γ . Lines r , s and t contain sides A B , A C and B C , respectively. Point I is the intersection between the tangent line to γ passing through A and the line t ; points H and K are defined similarly, as shown in figure.
If I H = H K then find the ratio B C A B , rounded to the nearest thousandth.
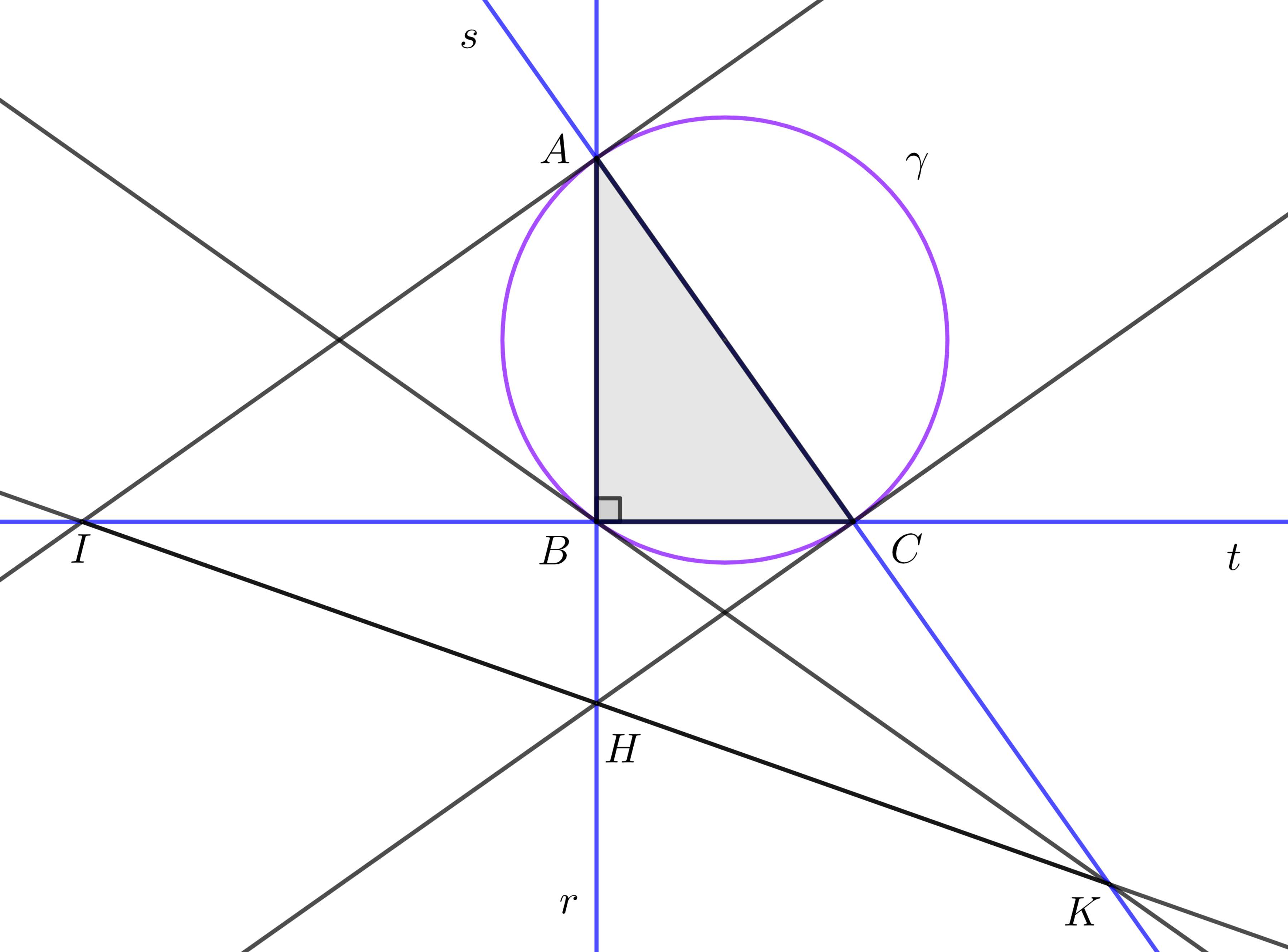
The answer is 1.414.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
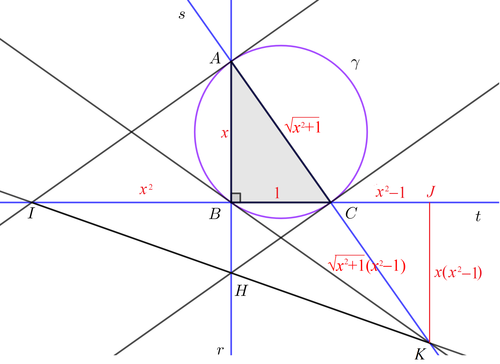 Let
B
C
=
1
and
A
B
=
x
. Then
B
C
A
B
=
x
. Since
△
A
B
C
and
△
A
B
I
are similar,
B
I
=
x
2
. Let
J
K
be perpendicular to line
t
. Then
△
I
J
K
and
△
I
B
H
are similar. If
I
H
=
H
K
, then
I
B
=
B
J
=
x
2
and
C
J
=
x
2
−
1
. Since
△
A
B
C
and
△
C
J
K
are similar,
J
K
=
x
(
x
2
−
1
)
.
Let
B
C
=
1
and
A
B
=
x
. Then
B
C
A
B
=
x
. Since
△
A
B
C
and
△
A
B
I
are similar,
B
I
=
x
2
. Let
J
K
be perpendicular to line
t
. Then
△
I
J
K
and
△
I
B
H
are similar. If
I
H
=
H
K
, then
I
B
=
B
J
=
x
2
and
C
J
=
x
2
−
1
. Since
△
A
B
C
and
△
C
J
K
are similar,
J
K
=
x
(
x
2
−
1
)
.
By tangent-secant theorem , we have:
B K 2 B J 2 + J K 2 x 4 + x 2 ( x 2 − 1 ) 2 x 4 + x 6 − 2 x 4 + x 2 x 6 − x 4 + x 2 x 4 = 2 x 2 x = C K ⋅ A K = C K ( A C + C K ) = x 2 + 1 ( x 2 − 1 ) ( x 2 + 1 + x 2 + 1 ( x 2 − 1 ) ) = ( x 2 + 1 ) ( x 2 − 1 ) x 2 = x 6 − x 2 = 2 ≈ 1 . 4 1 4
Well I think there no need to draw an extra line. First, assume that BC = 1 and AB = x (x > 0). Prove that HC is the midline of △AIK (since HC and AI are both perpendicular to AC, IH = HK), which let to AC = CK. Then prove that B is the centroid of △AIK -> BC/CI = 1/3. Since BC = 1 => IB = 2. Now prove that △ABC and △IBA are similar, then IB/BA = AB/BC, which is 2/x = x/1 => x^2 = 2 => x = 1.414213562...
How do you know that points I , H , K are collinear?
Draw J K perpendicular to line r , and let A B = b and B C = 1 .
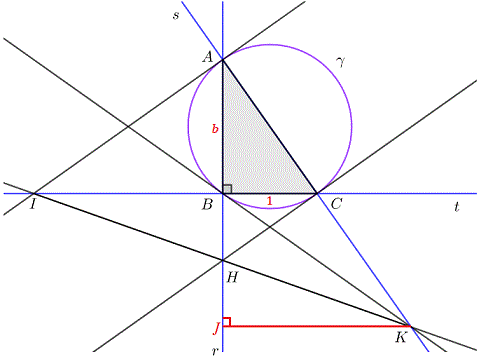
△ I B A ∼ △ A B C by AA similarity, so A B I B = B C A B , or b I B = 1 b , which solves to I B = b 2 .
△ C B H ∼ △ A B C by AA similarity, so B C B H = A B B C , or 1 B H = b 1 , which solves to B H = b 1 .
Since ∠ A B C is a right angle, A C is the diameter of circle γ , and its diameter is at the midpoint of A C which is ( 2 1 , 2 1 b ) . The slope of the radius through B is therefore b , which means B K has an equation of y = − b 1 x . A K has an equation of y = − b x + b , so K has coordinates ( b 2 − 1 b 2 , − b 2 − 1 b ) . Since I B = b 2 and B H = b 1 , I has coordinates ( − b 2 , 0 ) and H has coordinates ( 0 , − b 1 ) , and both the slopes of I H and H K calculate to − b 3 1 . Therefore, I , H , and K are collinear.
△ H J K ≅ △ H B I by AAS congruence, so H J = B H = b 1 and J K = I B = b 2 .
△ A J K ∼ △ A B C by AA similarity, so J K A J = B C A B , or b 2 b + b 1 + b 1 = 1 b , which rearranges to ( b 2 + 1 ) ( b 2 − 2 ) = 0 , and solves to b = 2 for positive real b .
Therefore, the ratio B C A B = 1 b = 2 ≈ 1 . 4 1 4 .
Don't you have to prove that points I , H , K are collinear?
Log in to reply
Good point! Coordinate geometry can be used to show that I H and H K have the same slope, which I have now included in my solution.
I solved this using similar triangle proportionality. Since we know that IH = HK then we know that triangle AIK has double the side lengths of triangle CHK. That makes AI = 2(CH). The tangent lines passing through line S are parallel making triangle AIB similar to triangle HCB with a scale factor of 2. Both of these triangles are similar to triangle ABC by angle-angle similarity. We can establish the proportional relationship as A B I B = B C A B . After cross multiplying we get that AB^2 = IB(BC). Because triangle AIB is twice the size of HCB, IB = 2(BC). By substitution AB^2 = 2BC^2. That makes AB/BC = root 2 or 1.414.
First thing first, I , H , K are collinear for any △ A B C . It is a direct consequence of the Pascal's theorem applied to the degenerate hexagon ( A A B B C C ) . Maybe inversion provides better proof anyway.
To the prob. Since, A I , C H both are tangents to the circle and A C is a diameter so, we have A I ∣ ∣ C H ⇒ A C = C K Let N denote the midpoint of A B then C N ∣ ∣ K H ⇒ ∠ B C N = ∠ K B C = ∠ A ⇒ B C 2 = B N × B A = 2 1 A B 2 ⇒ B C A B = 2 = 1 . 4 1 4 4 □
Let KB and AI intersect at D.Then using Newton-gauss lemma on the complete quadrilateral ABCD we find that,the midpoint of CD lie on AB since H is the midpoint of IK.Let that midpoint be X.Now,using some trig we get BD= 2 c o s ( C ) A C s i n ( C ) . But again from trinagle BCD we get , D X C X = A C c o s C B D s i n C = 1 . Then, using these two eqaution we get,cosC= 3 1 .The rest is simple.
Let the position coordinates of A , B and C be ( 0 , c ) , ( 0 , 0 ) and ( a , 0 ) respectively. Then the equation of the circle is x 2 + y 2 − a x − c y = 0 . Slope of the tangent to this circle at any point ( h , k ) is c − 2 k 2 h − a . Using this, the equation of A I is y = c a x + c 2 , and the position coordinates of I are ( − a c 2 , 0 ) . Similarly, the position coordinates of H and K are ( 0 , − c a 2 ) and ( c 2 − a 2 a c 2 , c 2 − a 2 − a 2 c ) respectively. Hence the condition ∣ I H ∣ = ∣ H K ∣ yields c 2 = 2 a 2 ⟹ a c = 2 ≈ 1 . 4 1 4
Let O be the centre of circle that will be on side AC. Let OA = OB = OC = R Side CH and AI both will be parallel. So, (KH/KI = KC/AK = 1/2) So, (AK = 2KC) So, (AK = 2(AK-AC) So, (2AC = AK) As, (AC = 2R) So, (AK= 4R) Hence, KC = 2R. Let angle ACB = X So, Angle OBC = OCB = X Hence Angle BOC = 180-2X In Triangle OBK Cos(180-2X) = R/3R = 1/3 -Cos(2X) = 1/3 Cos(X) = 1/1.732 Tan(X) = 1.414 Also, Tan(X) = AB/BC = 1.414
Let B C = 1 and B C A B = α ⇒ A B = α . We see that △ I A C ∼ △ A B C ∼ △ I B A ∼ △ C B H .
So B A I B = B C A B ⇒ I B = α 2 . Also, B C B H = B A B C ⇒ B H = α 1
From I B and B H we get I H 2 = I B 2 + B H 2 = α 4 + α 2 1
A H = A B + B H = α + α 1 ⇒ A H 2 = α 2 + α 2 1 + 2
Since △ I A K is right angled at A and H is the mid point of hypotenuse we get that H is the circumcentre of the △ I A K ⇒ I H = A H ⇒ I H 2 = A H 2 Now putting the I H and A H from above we get
α 4 + α 2 1 = α 2 + α 2 1 + 2 α 4 − α 2 − 2 = 0 ⇒ ( α 2 − 2 ) ( α 2 + 1 ) = 0 ⇒ α 2 = 2 ⇒ α = 2 .
Hence B C A B = 2 = 1 . 4 1 4