No need of any jugglery - 2
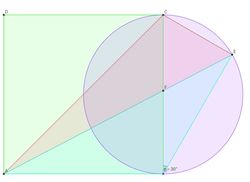 Given that
is a square of side length
.
is a point on the circumference of the circle with
as diameter such that
equals to
. The areas of
and
are
and
respectively. Find
where
represents the greatest integer lesser than or equal to
.
Given that
is a square of side length
.
is a point on the circumference of the circle with
as diameter such that
equals to
. The areas of
and
are
and
respectively. Find
where
represents the greatest integer lesser than or equal to
.
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There's a typo in the problem. It should read: E is a point on the circumference of the circle with BC as diameter. With the centre of the circle as the origin, the circle is: x² + y² = 9, while BE is: y=√3 x -3. E can now be easily determined as [ 2 3 √ 3 , 2 3 ], A:[-6.-3] and C:[0,3]. Sum of the areas of Tr. ACE & Tr. ABE = 25.794