No need of any jugglery

Geometry Level 3

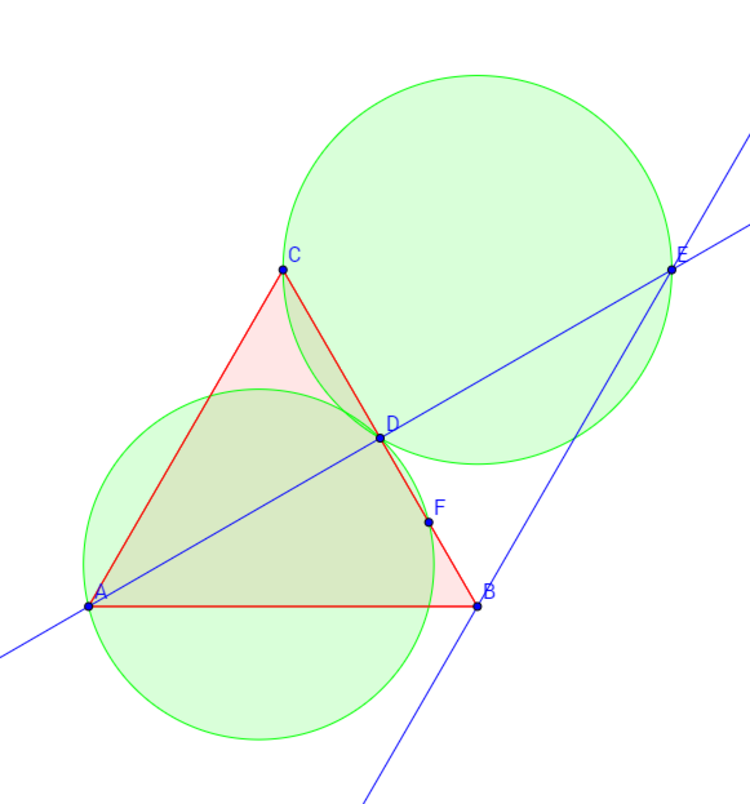Given is an equilateral $\Delta ABC$ . $BE$ is parallel to $AC$ and intersects $AD$ produced at $E$ where $D$ is the midpoint of $BC$ . $F$ is the midpoint of $BD$ . Find the ratio of radius of circle circumscribing $\Delta CDE$ to that of the circle circumscribing $\Delta ADF$ . Provide your answer up to three decimal places.

The problem is original. You may also try this one .

The answer is 1.109.

1 solution

Niranjan Khanderia
May 17, 2015

. $ABEC~ is ~a ~parallelogram. ~ \therefore~CE=AB.\\ \angle~CDE~=90^o~\implies~EF~is~diameter~of ~circle ~circumscribing~\Delta ~CDE.\\In~circle ~circumscribing~\Delta ADF, ~\angle ADF=90^o~\implies~AF~is~diameter.\\AF=\sqrt{AD^2+DF^2}=\sqrt{ (\dfrac{\sqrt 3} { 2 }*AB)^2+(\dfrac 1 4 *AB)}=\dfrac {\sqrt{13}} 4 *AB \\ \implies~requiered~ ratio= ~~~~~~\dfrac 4 {\sqrt{13}}=~~~~\color{#D61F06}{1.109}\\~~~\\$
Side length is given as 6, but it is not required.

Nice method sir! I have edited the problem. There is a typo in the second and fourth line of your solution.

Rohit Ner - 6 years ago

Thanks both for your appritation and correction.

Niranjan Khanderia - 6 years ago

No need of any jugglery

The problem is original. You may also try this one .

The answer is 1.109.

1 solution

0 pending reports