This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
this is exactly how i solved this
In fact extending the above argument it is easy to see that f ( 1 ) < 0 and f ( − 1 ) < 0 are necessary and sufficient for the roots of the quadratic to be in ( − ∞ , − 1 ) and ( 1 , ∞ ) . Hence, m 2 − 8 < 0 and m 2 + 2 m − 6 < 0 , which implies that m ∈ ( − 2 ( 2 ) , 2 ) . Thus the only integer values that are acceptable are { − 2 , − 1 , 0 , 1 } giving the answer as 4 and not 5 .
Using the discriminant for the polynomial: (m + 1)^2 -4(m^2 + m - 8) >= 0 to have real solutions. This gives -11/3 <= m <= 3. This gives 7 possible integral m solutions. All integers in that range, except for 3 and -3 since they give roots of multiplicity 2 for m = 3 and solutions both less than 1 for m = -3. Hence, 5 solutions.
Pal you may have used latex your answer would look more beautiful. I am not a moderator thus I can not latexify it.
Log in to reply
Sorry... I have no knowledge of using LaTex...
Log in to reply
Then use "Daum Equation Editor" in Chrome Browser.
Using the discriminant for the polynomial:
(
m
+
1
)
2
−
4
(
m
2
+
m
−
8
)
>
=
0
to have real solutions. This gives
3
−
1
1
<
=
m
<
=
3
. This gives 7 possible integral m solutions. All integers in that range, except for 3 and -3 since they give roots of multiplicity 2 for m = 3 and solutions both less than 1 for m = -3. Hence, 5 solutions.
As desired by Parth Lohomi .
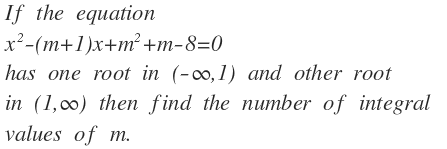
Let the roots of the equation be a , b where a < b
Now, according to the problem a < 1 and b > 1
And, we know that, since the leading coefficient is positive, the graph of the given quadratic must be a parabola (concave upwards).
Now, from this, we arrive at the conclusion that f ( 1 ) < 0
For instance, the graph will be something like -
(Thus, the graph clearly suggests that since one root is grater than 1 and other being less than 1, f ( 1 ) must necessarily be negative)
Thus, f ( 1 ) = 1 − ( m + 1 ) + m 2 + m − 8 < 0 m 2 − 8 < 0 ( m − 2 2 ) ( m + 2 2 ) < 0 ⇒ − 2 2 < m < 2 2
Therefore, the only possible integer values of m are ( − 2 , − 1 , 0 , 1 , 2 ) which gives total 5 integral values for m
(Note - The original graph may be completely different. I've used this graph just to demonstrate about the behaviour of the given quadratic function)