Collision Fun!!

Classical Mechanics Level 5

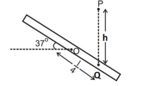
A uniform smooth rod of mass $M = 2.5 \text{ kg}$ and length $l = 4 \text{ m}$ is lying still on a smooth horizontal table. Now I shoot a small ball of mass $m = 2 \text{ kg}$ from point $P$ such that it traces the path shown and hit the rod at a distance of $l / 4$ from the centre. The ball collides elastically with the rod. Let $\omega$ represents the angular velocity of the rod just after collision and ${v}_\text{rel}$ represents the relative velocity of ball just after collision with respect to centre of mass of the rod.

Find ${v^2}_\text{rel} \times \omega$ .

Details and Assumptions :

The ball was given an impulse $I = 20 \text{ kg m/s}$ at point $P$ .
Consider the figure for geometry.
Friction is absent everywhere.
The rod is completely free (that is free to do translational as well as rotational motion).

This is Original

This is a part of my set Aniket's Level 5 Challenges in Classical Mechanics .

The answer is 208.0.

2 solutions

Aniket Sanghi
Aug 17, 2016

The main thing about this question is to choose the plane and directions to solve . The solution becomes much simpler if you choose the direction along rod and perpendicular to rod to solve.

Parameters used are v is velocity of particle before collision . ( this velocity is resolved into components along rod and perpendicular to rod).

v' is the component of velocity of particle in the direction perpendicular to rod . Velocity component along direction of rod remains same as in that direction no impulse is applied by rod ( since rod is smooth )

After finding $\omega$ rest all you can easily find :) .

I hope you like the question as well as solution :).

Yeah nice solution!

Prakhar Bindal - 4 years, 10 months ago

But that thing stroke my mind originally therefore that was my thought but will remember this thing always to choose directions carefully!

Prakhar Bindal - 4 years, 10 months ago

Did the same! Nice problem :p

Sumanth R Hegde - 4 years, 2 months ago

Prakhar Bindal
Aug 17, 2016

Its a nice question but yeah involves a bit of hardwork

Here are some terms which i am defining in my solution

Let the rod move with an angular velocity w , Centre of mass move with horizontal velocity vx' to the left and with vertical velocity vy' downwards

Similarly let ball with velocity vx towards right and vy downwards.

We will use Impulse Momentum theorem to solve the problem

Call the impulse between the ball and the rod to be Ndt which will act normal to the rod

Using Impulse Momentum theorem in 2 directions on two objects (ball and rod) will yield us 4 equations

Considering Angles carefully you will get the equations as

4Ndt/5 = 20-2vy

3Ndt/5 = 2vx

4Ndt/5 = 2.5vy'

3Ndt/5 = 2.5vx'

Now using Angular equivalent of above theorem about centre of mass

Ndt * L/4 = 2.5 16 w / 12

On putting values you obtain

Ndt = 10w/3

Now we have one more information that coefficient is perfectly elastic

So using coefficient of restitution equation

(This has to be written carefully as it will contain many terms)

On carefully considering velocities we get

e = v2-v1 / u1-u2

Here subscript 2 signifies rod and 1 signifies ball

u2 = 0 , u1 = 8 , v2 = Lw/4 + 4vy'/5 + 3vx'/5

v1 = 4vy/5-3vx/5

e = 1

Now putting in above equation and solving all above equations simultaneously you will get following values

Ndt = 40/3

w = 4

vy = 14/3

vx = 4

vx' = 16/5

vy' = 64/15

Asked term relative velocity can be easily found out using vectors (but be careful with directions again)

Solving and value of asked term comes exactly = 208.00000000000

Brilliant Question Again!

This solution can be much simplified if you take velocity components along direction of rod and perpendicular to rod .

Aniket Sanghi - 4 years, 10 months ago

Bro! @Prakhar Bindal , Check my solution once . It can be solved in just 3 equations !!! :)

Aniket Sanghi - 4 years, 10 months ago

u1 !=8 as m=2 and not 2.5 u1 = 10

A Former Brilliant Member - 4 years, 9 months ago

Collision Fun!!

This is a part of my set Aniket's Level 5 Challenges in Classical Mechanics .

The answer is 208.0.

2 solutions

0 pending reports