No Problemmo #10
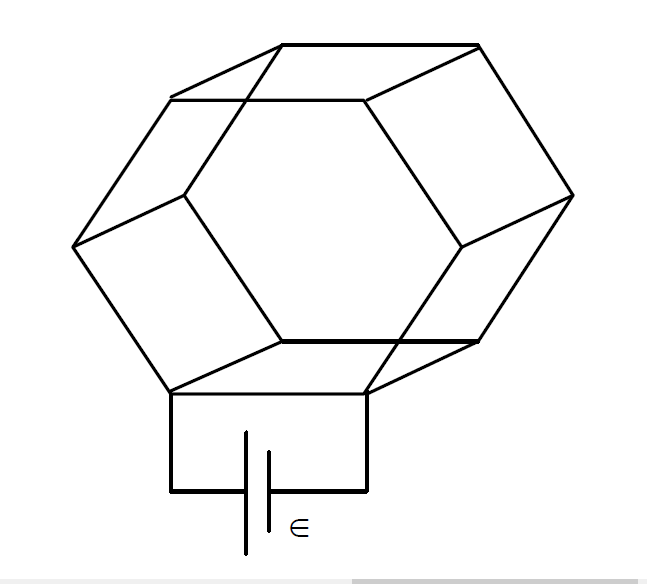
An electrical network of wires is formed by joining the grid points of two hexagons, as shown, where the resistance of each side and the connecting wires is An ideal battery of emf is joined at the bottom.
Considering that the wire connected with the cell is ideal, find the current passing through the battery.
Take and
For more exciting problems, try my set No Problemmo .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider these currents on the loops
By kirchoff's voltage law (closed loops) we have that:
⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ R − R 0 0 0 0 0 − R 4 ∗ R − R 0 0 0 − R 0 − R 4 ∗ R − R 0 0 0 0 0 − R 4 ∗ R − R 0 0 0 0 0 − R 4 ∗ R − R 0 0 0 0 0 − R 4 ∗ R − R 0 − R 0 0 0 − R 4 ∗ R ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⋅ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ I 1 I 2 I 3 I 4 I 5 I 6 I 7 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ V 0 0 0 0 0 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ Solving this with your favorite method, mine is Cramer's rule, and we get that I 1 = 2 . 5 7 8 1 2 5 or I 1 ≈ 3 rounding to the nearest integer.