No red allowed
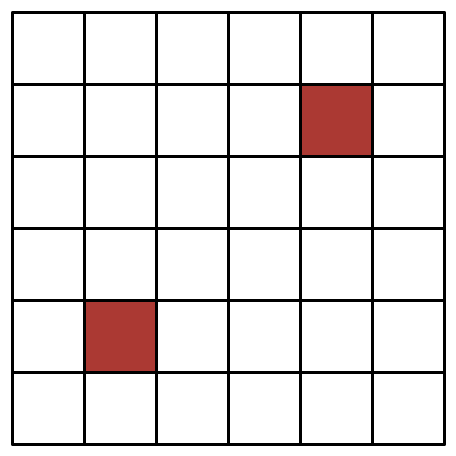 In the above image, how many rectangles are there which
do not
include any red squares?
In the above image, how many rectangles are there which
do not
include any red squares?
The answer is 257.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Yes. Isn't it nice how there's such a simple way to count? Anyone that tried to list out all the possible rectangles would have had a hard time to get to 257.
Log in to reply
That's the beauty of mathematics... First it teaches us to count, then it teaches us to logically count... :-)
Yes, it was very hard for me to count all 257...
Interesting, I counted the number of rectangles that could be created in the 4 × 4 squares in the bottom right and top left then the squares formed in each corner. This is a much nicer method.
Log in to reply
This requires a tedious method of partitions of the set by which I couldn't get the answer
Log in to reply
See Andrea's solution below. Once you commit to doing it tediously, the case work isn't that bad. Trying to be "smart" about it makes the count trickier.
We will use the inclusion-exclusion principle: The answer is (all rectangles) - 2(rectangles containing the red square in the top right) + (rectangles containing both squares) = ( 2 7 ∗ 6 ) 2 - 2 * 25 * 4 + 4 * 4 = 257. ) To understand this way of counting, draw a Venn diagram! To count all rectangles, we observe that there are ( 2 7 ) = 2 7 ∗ 6 = 2 1 choices for the left and the right edges and as many for the lower and the upper edges. To count the rectangles that contain the red square in the top right, note that there are 25 choices for the lower left corner and 4 choices for the upper right corner. (The lower left corner has to be to the left and below the red square, while the upper right corner has to be to the right and above.) By symmetry, there are just as many rectangles (namely, 100) containing the red square in the lower left. Likewise, for the rectangles containing both squares there are 4 choices for the lower left corner as well as for the upper right corner.
Thanks! I made a mistake with the counting, and so was off by 8.
Log in to reply
Same here(at first)
I found 265
This method of looking at corners is quite interesting.
I've simply counted all the possible rectangles with area 1(1×1),2(1×2),3(1×3),4(1×4 or 2×2)..and so on..that do not include the two red squares. It's very simple and due to the symmetry of the two red squares for example rectangles 1×3 are as many as rectangles 3×1. 34+52+40+28+17+16+8+24+14+8+4+2+8+2=257
Simple works too :)
I tried this but forgot to count the squares, (1x1, 2x2 ...)
Let the Horizontal lines from bottom to top be h 0 , h 1 , . . . , h 6 and Vertical lines from left to right be v 0 , v 1 , . . . , v 6
Total Rectangles = 7 C 2 × 7 C 2 = 4 4 1
Rectangles that contain bottom left red square is all rectangles that can be formed by choosing one horizontal line from { h 0 , h 1 } , another horizontal line from { h 2 , . . . , h 6 } and one vertical line from { v 0 , v 1 } , another vertical line from { v 2 , . . . , v 6 } .
Total number of rectangles that contain bottom left red square = ( 2 C 1 × 5 C 1 ) × ( 2 C 1 × 5 C 1 ) = 1 0 0
Similarly, total number of rectangles that contain top right red square = ( 2 C 1 × 5 C 1 ) × ( 2 C 1 × 5 C 1 ) = 1 0 0
Total number of rectangles that contain both the red squares are all the rectangles that can be formed by choosing one horizontal line from { h 0 , h 1 } , another horizontal line from { h 5 , h 6 } and one vertical line from { v 0 , v 1 } , another vertical line from { v 5 , v 6 } .
Total number of rectangles that contain both the red squares = ( 2 C 1 × 2 C 1 ) × ( 2 C 1 × 2 C 1 ) = 1 6
From principle of inclusion-exclusion:
Rectangles without any red squares = 4 4 1 − ( 1 0 0 + 1 0 0 − 1 6 ) = 2 5 7