No right angles?
In icosahedron is a regular solid with 20 triangular faces, connecting 12 identical vertices:
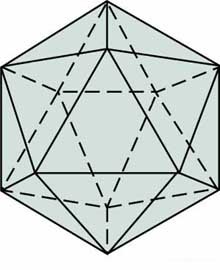
Consider the directions defined by the 30 edges of the icosahedron. Are any of these directions perpendicular to each other?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Each edge is parallel to its antipode (the edge directly across). Thus the edges define 15 different directions in space. These can be divided into five sets of three mutually perpendicular directions.
One way to see this is by viewing the icosahedron along the perpendicular bisector of one of the vertices:
Marked in red are three pairs of edges in perpendicular directions. (The horizontal segment represents two edges, one directly behind the other. The red dots represent two edges that run directly "into the paper".)
Alternatively, an icosahedron can be described by coordinates ( 0 , ± 1 , ± ϕ ) ; ( ± ϕ , 0 , ± 1 ) ; ( ± 1 , ± ϕ , 0 ) , where ϕ = 2 1 ( − 1 + 5 ) is the golden ratio. Two points are connected iff their distance equals two units. Thus, the points ( 0 , ± 1 , ϕ ) ; the points ( ϕ , 0 , ± 1 ) ; and the points ( ± 1 , ϕ , 0 ) describe edges that run parallel to the y -, z - and x -axis, respectively.