No slide rule required!
The curve given parametrically by
and
intersects itself (as shown in the figure below). Find the sum of the coordinates at the point of intersection.
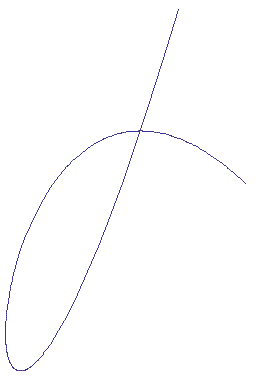
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There must be 2 different values of the parameter t which yields the same x , so first we solve the quadratic equation for t
t 2 − t = x
with solutions
t 1 = 2 1 ( 1 − 1 + 4 x )
t 2 = 2 1 ( 1 + 1 + 4 x )
We plug those into the equation for y
t 1 3 − 3 t 1 = t 2 3 − 3 t 2
Simplifying, we end up with
( x − 2 ) 1 + 4 x = 0
or x = 2 , and we quickly find y = 2 , so that the answer is 2 + 2 = 4