No sliding.
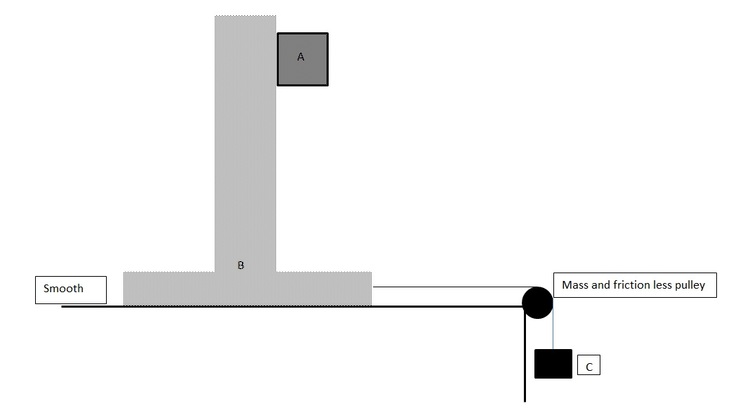 In the arrangement shown in the figure mass of the block B and A are 2m,8m respectively and the floor is smooth. The block B is connected to block C by means of a pulley. If the whole system is released then the minimum value of mass of the block C so that block A remains stationary with respect to B is:
In the arrangement shown in the figure mass of the block B and A are 2m,8m respectively and the floor is smooth. The block B is connected to block C by means of a pulley. If the whole system is released then the minimum value of mass of the block C so that block A remains stationary with respect to B is:
Details:
1.Co-efficient of friction between A and B is
2.No friction between B and floor.
Please Post Solutions also.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For A to remain stationary with respect to B, friction and it's weight should cancel out i.e. μ N = ( 8 m ) g ; where N is the normal force by B's surface to A and they should have the same acceleration.
N will have the magnitude but opposite direction of pseudo force due to it's acceleration.
N = (8m) x ¨ .
Thus,
μ ( 8 m ) x ¨ = ( 8 m ) g
x ¨ = μ g
Now the system of A and B is connected to C by an inextensible string. So for A and B to accelerate at x ¨ C should also accelerate at x ¨ .
The force for the whole system A,B and C to accelerate at x ¨ is thw weight of C.
So the force equation is
( 8 m + 2 m + M ) x ¨ = M g ; M is the mass of C.
x ¨ = 1 0 m + M M g
So,
μ g = 1 0 m + M M g
M = μ − 1 1 0 m .
This is the minimal solution of M as increasing it will only cause to increase in the normal force N which increases limit of the friction then required.