No Slip Sliding Away
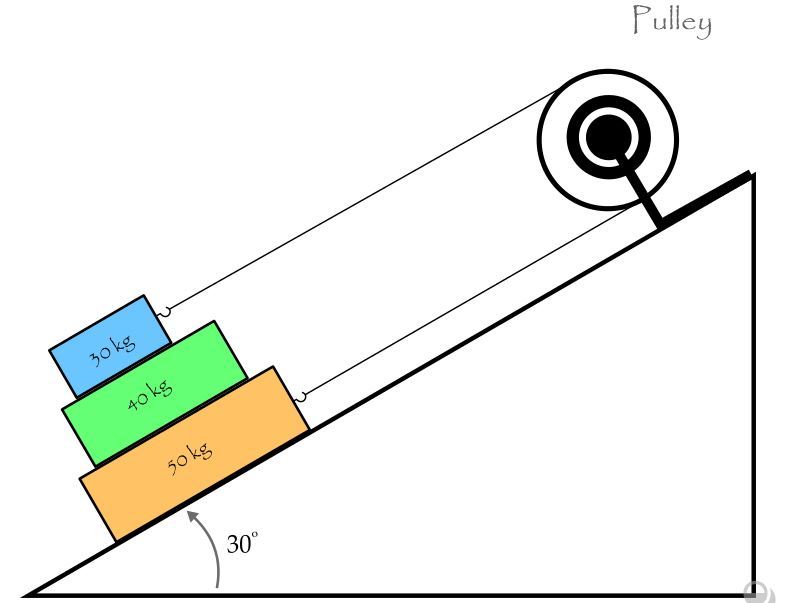
Three blocks placed on top of each other are on a plane inclined at an angle of 3 0 ∘ with respect to horizontal. The top and bottom blocks are connected by a string that goes over a pulley. The top block has a mass of 3 0 kg , the middle one a mass of 4 0 kg , and bottom one a mass of 5 0 kg .
If the coefficient of static friction μ s is the same between all the pairs of surfaces, then find the minimum value of μ s such that the blocks remain in equilibrium.
Give your answer to 3 decimal places.
The answer is 0.231.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Fantastic! I basically used the same approach (but considered the masses separately, instead of grouping them).
There would be 2 values of
μ
coming but we have to consider the one for which the 40 kg block does'nt slip !
i'll be adding a force diagram to help u understand the directions of friction(as some people r having trouble considering the frictions) and the other forces hope it helps!/...........
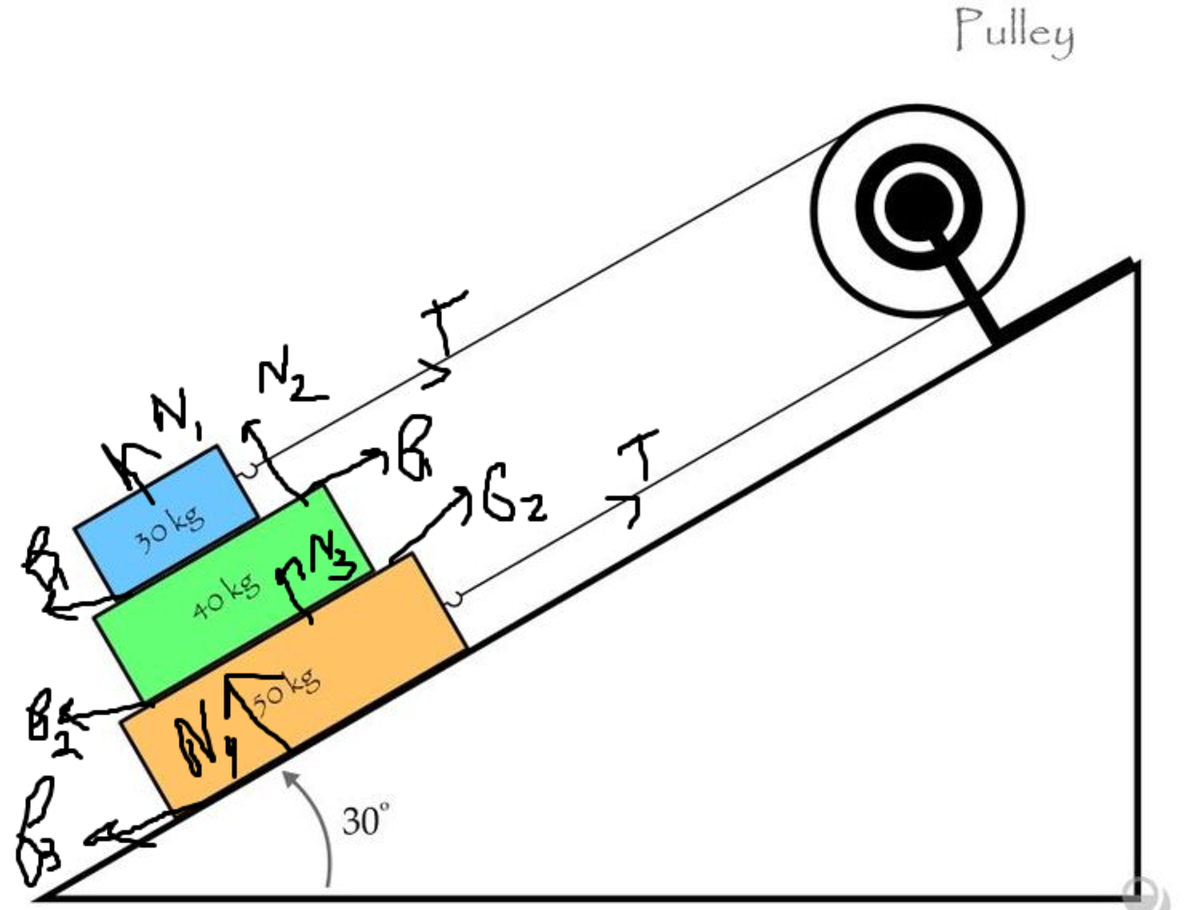 force-body diagram !!
i have considered the forces keeping in mind u get a minimum co-efficient of friction !
force-body diagram !!
i have considered the forces keeping in mind u get a minimum co-efficient of friction !
upvote and like !!
Log in to reply
upvote and like !! --->done :)
Please tell how to draw mechanics diagram at brilliant?
From where you draw this diagram? Which website?
| Disclaimer : Read Mark Hennings comment below for why this solution doesn't work in all scenarios. |
A system is in equilibrium if all its parts have a net force of zero, so we can just consider the force on the middle block.
Let N 1 be the normal force on the 40 kg block from the 30 kg block and let N 2 be the normal force on the 40 kg block from the 50 kg block.
We know that f ≤ μ s ( N 1 + N 2 ) where f is the total force of friction (from top and bottom surfaces). Adding the force of gravity in the direction of the slope ( − 2 0 0 N ) to each side of that equation, we get: F ≤ μ s ( N 1 + N 2 ) − 2 0 0 ( 1 )
where F is the total force.
Now let's calculate N 1 and N 2 :
N 1 = 3 0 g sin 3 0 ∘ = 2 3 3 0 g = 1 5 3 g = 1 5 0 3
and N 2 = N 1 + 4 0 g sin ( 3 0 ∘ ) = 1 5 0 3 + 2 0 0 3 = 3 5 0 3
Plugging these into (1) and setting F = 0 (because of equilibrium):
0 ≤ μ s ( 1 5 0 3 + 3 5 0 3 ) − 2 0 0 = 5 0 0 μ s 3 − 2 0 0 ⟹ μ s ≥ 5 3 2
This implies the minimum value of μ s is 5 3 2 or 0.23094010767 .
I think you still need to check what is going on at the slope. You are quite right that ensuring that the friction requirements are satisfied at both the top and the bottom of the middle block requires that μ ≥ 5 3 2 . However, until we check, it could be the case that friction is also limiting at the slope, which could allow for a situation where the top and bottom blocks are moving (the middle block could be in limiting equilibrium with respect to both upper and lower blocks, but sliding against one, which stationary with respect to the other). If that happened, we would need a higher value of μ to have equilibrium.
It is because we have nonlimiting equilibrium at the slope for this critical value of μ that the result holds.
Log in to reply
This is a good point, thanks. I'll edit my solution and mention this comment.
How is 3 0 g sin 3 0 o = 1 5 0 3
Suppose that the normal reaction and friction force between the 3 0 kg and 4 0 kg blocks are R 1 , F 1 , that the normal reaction and friction forces between the 4 0 kg and the 5 0 kg blocks are R 2 , F 2 , and that the normal reaction and friction forces between the 5 0 kg block and the slope are R 3 , F 3 .
Resolving forces on the 3 0 kg block perpendicular and parallel to the slope, we see that R 1 = 1 5 g 3 T + F 1 = 1 5 g Treating the 3 0 kg and 4 0 kg blocks as a single object, and resolving forces similarly, we see that R 2 = 3 5 g 3 T + F 2 = 3 5 g Treating the three blocks as a single object, and resolving forces, we see that R 3 = 6 0 g 3 2 T + F 3 = 6 0 g Since ∣ F 1 ∣ ≤ μ R 1 , ∣ F 2 ∣ ≤ μ R 2 , ∣ F 3 ∣ ≤ μ R 3 , we deduce that T must lie in the intersection of the three intervals [ 1 5 g − 1 5 g 3 μ , 1 5 g + 1 5 g 3 μ ] [ 3 5 g − 3 5 g 3 μ , 3 5 g + 3 5 g 3 μ ] [ 3 0 g − 3 0 g 3 μ , 3 0 g + 3 0 g 3 μ ] If μ ≥ 3 1 , then T = 0 is a possible solution, so the string and pulley are not necessary. Let us suppose that μ < 3 1 so that all these intervals are subsets of ( 0 , ∞ ) . Then the intersection of these three intervals is [ 3 5 g − 3 5 g 3 μ , 1 5 g + 1 5 g 3 μ ] (with the largest left-hand end and the smallest right-hand end) provided that 3 5 g − 3 5 g 3 μ ≤ 1 5 g + 1 5 g 3 μ , which happens when μ ≥ 5 3 2 . Otherwise, the intersection is empty. This makes the smallest possible value of μ equal to 0 . 2 3 0 9 4 0 1 0 8 .
Note that, at this smallest possible value of μ = 5 3 2 , friction is limiting between the 3 0 kg and 4 0 kg blocks, and between the 4 0 kg and 5 0 kg blocks (but not between the 5 0 kg block and the slope). Thus, for a slightly smaller value of μ , the 4 0 kg block will slide out between the 3 0 kg and 5 0 kg blocks.