I Was Very Amazed At The Solution 10
Evaluate:
x = 4 5 ∑ 8 9 cot ( x ∘ ) − x = 4 6 ∑ 8 9 ( cot ( 2 x ∘ ) + csc ( 2 x ∘ ) )
For more problems like this, try this set .
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
This is the story where the problem comes from.
∫ sec ( x ) − 1 1 dx = ∫ 1 − cos ( x ) cos ( x ) dx = ∫ ( − 1 + 1 − cos ( x ) 1 ) dx = − x + ∫ 1 − cos ( x ) 1 dx = − x + ∫ sin 2 ( x ) 1 + cos ( x ) dx = − x + ∫ csc 2 ( x ) dx + ∫ cot ( x ) csc ( x ) dx = − x − cot ( x ) − csc ( x ) + C
Meanwhile, the answer and solution of this problem to other sites is different. They use tangent-half angle substitution and double angle formula and obtaining − x − cot ( 2 x ) + C ⋅ Since the 2 answers came from the same integrand, the answers must be equivalent and hence, cot ( x ) + csc ( x ) = cot ( 2 x ) + C ⋅ Putting any value for x , you will obtain C = 0 ⟹ cot ( x ) + csc ( x ) = cot ( 2 x ) , and by induction, cot ( 2 x ) + csc ( 2 x ) = cot ( x ) ⟹ − cot ( 2 x ) − csc ( 2 x ) + cot ( x ) = 0 ⟹ x = 4 5 ∑ 8 9 cot ( x ) − x = 4 6 ∑ 8 9 ( cot ( 2 x ) + csc ( 2 x ) ) = cot ( 4 5 ) = 1 ⋅
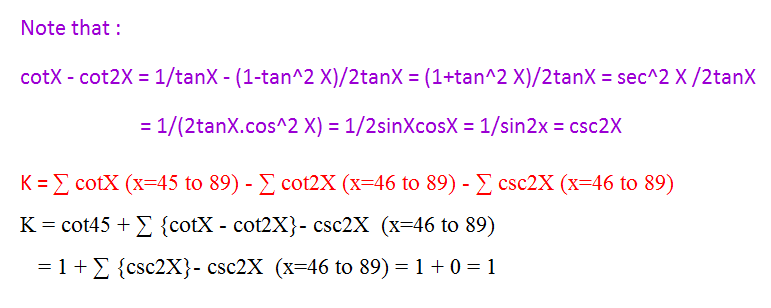
X = x = 4 5 ∑ 8 9 cot x ∘ − x = 4 6 ∑ 8 9 ( cot 2 x ∘ + csc 2 x ∘ ) = cot 4 5 ∘ + x = 4 6 ∑ 8 9 ( cot x ∘ − cot 2 x ∘ − csc 2 x ∘ ) = 1 + x = 4 6 ∑ 8 9 ( cot x ∘ − tan 2 x ∘ 1 − sin 2 x ∘ 1 ) = 1 + x = 4 6 ∑ 8 9 ( cot x ∘ − sin 2 x ∘ cos 2 x ∘ − sin 2 x ∘ 1 ) = 1 + x = 4 6 ∑ 8 9 ( cot x ∘ − sin 2 x ∘ cos 2 x ∘ + 1 ) = 1 + x = 4 6 ∑ 8 9 ( cot x ∘ − 2 sin x ∘ cos x ∘ 2 cos 2 x ∘ − 1 + 1 ) = 1 + x = 4 6 ∑ 8 9 ( cot x ∘ − sin x ∘ cos x ∘ ) = 1 + x = 4 6 ∑ 8 9 ( cot x ∘ − cot x ∘ ) = 1