This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Solving Triangles - Problem Solving - Medium
Nocturne No.2 Commentary
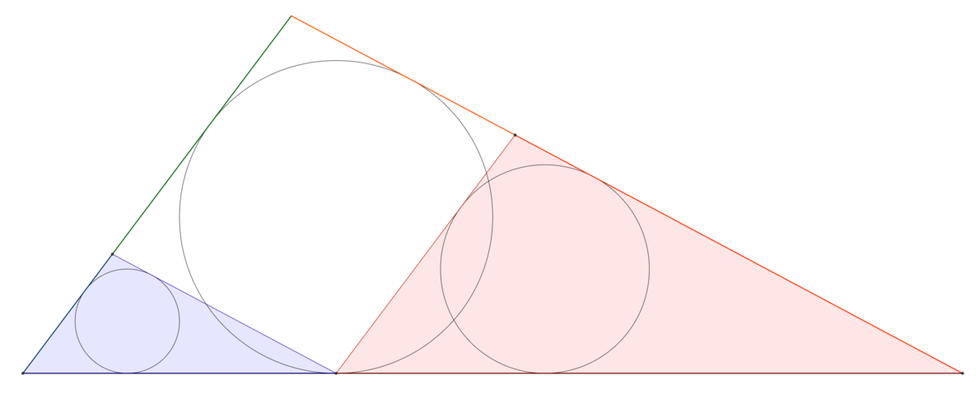
Notice how the blue, red and large triangles are similar.
Therefore, the ratio between the inradius and the length of the green side of each triangle is the same.
Also, the sum of the lengths of the green sides of the small triangles
is equal to the length of the green side of the large triangle.
Therefore, the sum of the inradii of the small triangles is equal to the inradius of the large triangle.