Altitude of Inscribed Triangle

Geometry Level 4

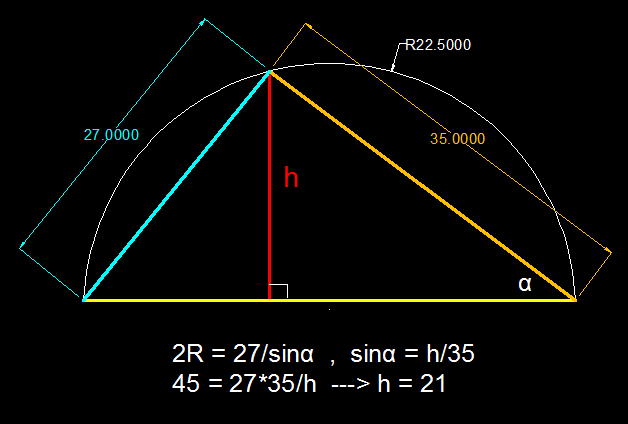
The above diagram shows a triangle with shorter sides of length 27 and 35, and its circumcircle with diameter 45.

Find the length of the purple perpendicular dropped to the base of the triangle.

Note: The diagram is not drawn to scale.


The answer is 21.

View wiki
Lolly Lau by Lolly Lau , 31, Hong Kong

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Lolly Lau
Nov 12, 2016

Nocturne No. 4 Commentary

A diameter in black and another chord in yellow has been drawn as shown.

Notice that the two marked angles are the same because they subtend the same segment.

Also, the angle opposite the diameter is a right angle (converse of Thales' theorem).

Therefore the length of the perpendicular can be found by solving sin ⁡ ( a n g l e \sin(\color{#D61F06}{angle} ) = 27 45 = p e r p e n d i c u l a r 35 )=\frac{27}{45}=\frac{\color{#69047E}{perpendicular}}{35} .

8 Helpful 0 Interesting 0 Brilliant 0 Confused

This is a very elegant solution. You might want to indicate briefly that because the marked angles are the same (also using the fact the inscribed angle in a semicircle is 90 degrees) you can use similar triangles. Ratios can happen in geometry problems for other reasons and I had to make an assumption what you were doing.

Jason Dyer Staff - 4 years, 7 months ago

Nice solution!

Peter van der Linden - 4 years, 7 months ago

A method I never though of ! Thanks.

Niranjan Khanderia - 4 years, 6 months ago
Ahmad Saad
Nov 12, 2016

4 Helpful 0 Interesting 0 Brilliant 0 Confused

Nice solution. +1)

Niranjan Khanderia - 4 years, 6 months ago

R = a b c 4 ∗ a r e a . ∴ 2 R = a b c 2 ∗ { 1 2 ∗ x ∗ c } , w h e r e x i s t h e r e q u i r e d p u r p l e p e r p e n d i c u l a r . x = a b c 2 ∗ 45 ∗ 1 2 ∗ c = 27 ∗ 35 45 = 21 R=\dfrac{abc}{4*area}.\\ \therefore\ \ \ 2R=\dfrac{abc}{2*\{\frac 1 2*x*c\}}, \ \ where\ x \ is\ the\ required\ purple\ perpendicular .\\ x=\dfrac{abc}{2*45*\frac 1 2*c}=\dfrac{27*35}{45}=\Large\ \ \ \ \color{#D61F06}{21}\ \\

2 Helpful 0 Interesting 1 Brilliant 0 Confused

The best and easiest solution

Valentin Duringer - 1 year, 3 months ago
Kelvin Hong
Nov 25, 2016

Draw a triangle ABC with AB=27 , AC=35 , We get A B s i n C = A C s i n B = 2 R \frac {AB}{sinC} = \frac {AC}{sinB} =2R

⇒ \Rightarrow 27 s i n C = 35 s i n B = 45 \frac {27}{sinC} = \frac {35}{sinB} = 45

⇒ s i n B = 35 45 \Rightarrow sinB = \frac {35}{45}

T h e n , h e i g h t = A B s i n B Then , height = AB sinB = 27 × 35 45 =27 \times { \frac {35}{45} } = 21 = \boxed {21}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...