Nocturne No.1

Nocturne No.1 Commentary

Notice how the purple area is half of the rectangle and half of the square.

Therefore the rectangle and the square have the same area.

The width of the rectangle can then be easily found to be .

Triangle ABG is similar to triangle BCE by AAA property. The rest is shown in figure.

Imgur

Note that the marked red and blue triangles are all similar. Thus, we obtain the ratio $\dfrac{25}{20}=\dfrac{20}{x}\implies x=\boxed{16}$ .

20×20÷25=16 ; This is one method.

In other method, for this diagram we can prove that The area of Square and Rectangle are equal. Hence b=16

Lol. Solved it using sine law. Clearly not clever enough to see that halfsies thing.

I wasn't sure so I hit 16 because it seemed likely and it was!

We can observe a triangle labelled x and z where we notice that :

Base = 1/2 * 25 = 12.5

and , hence the width (x) = 20^2 - (12.5)^2 <From Pythagoras Theorem

Hence x = 15.6 \approx 16 < Hence Answer

I just looked at it and thought the most common triangle is the 3-4-5 triangle. since the hypotinus was 20 I figured my best options were 12 and 16. Ta-da

The rightmost triangle is congruent to the upper left triangle. We see that the ratio of the hyptenuses is 5:4, and such the side similar to the width of the rectangle (being a side of the square) is 4/5 * 20, = 16

Personally I like solving problems with nice complex formulas so...

The Pythagorean Theorem can be used to find all the sides of the larger blue triangle (15,20,25 or a 3:4:5 ratio). You can prove that the top red triangle and larger blue triangle are similar through a Hypotenuse-Leg proof therefore allowing you to set the two triangles in ratio to one another or in ratio to 3:4:5. The width of the rectangle is the "4" in that ratio so let's use the given information (the length of the square) to finally set up our equation...

X/20=4/5

X=16

Ar(square)/length

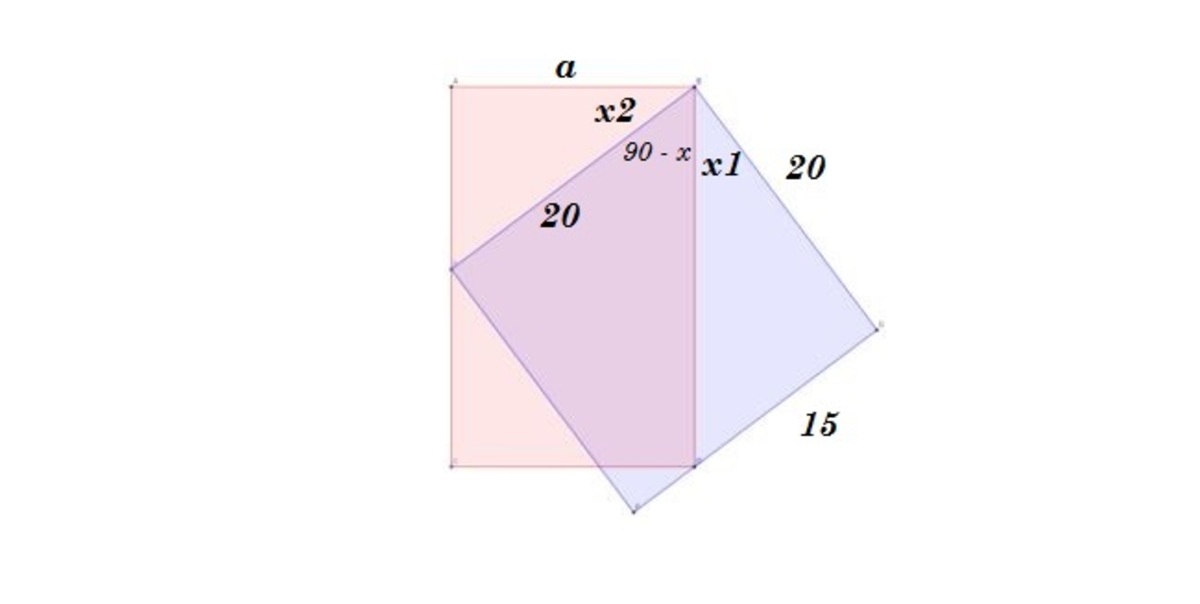
$x1 + (90 - x) = x2 + (90 - x) = 90$

so

$x1 = x2 = x$

$tan(x1) = \frac{15}{20} = 0.75 = tan(x)$

$a = 20 cos(x) = 20 cos( arctan (0.75) ) = \boxed{16}$