Nomadic tribe route
A nomadic tribe in the northern hemisphere moves along the following route every year:
- In spring, the tribe moves 100 km to the east.
- In summer, the tribe moves 100 km to the north.
- In autumn, the tribe moves 98 km to the west.
- In winter, the tribe moves 100 km to the south.
The tribe reaches its exact starting point from the spring and sets up its winter quarters there.
At what latitude ϕ are the winter quarters (in degrees)? Round to the nearest integer.
Note: Earth's radius is R = 6 3 7 1 km .
The answer is 52.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I have a question (I'm a beginner), do you consider the 100 km traveled from the y axis dimension or from the perimeter of the earth?
Log in to reply
The 100km are traveled on the perimeter, not on the y-axis. In the first attempt I did this wrong too :)
Is this the only solution? What if while moving eastbound, the tribe makes more than 360 degrees?
Log in to reply
You beat me to it. :-) There are an infinite number of solutions, though most of them are silly.
You think of solutions of the following kind: 1 0 0 km 9 8 km = 6 3 7 1 km ⋅ cos ( ϕ ) ( Δ λ + 2 π n ) = 6 3 7 1 km ⋅ cos ( ϕ + 0 . 0 1 5 7 ) ( Δ λ + 2 π m ) where n , m ∈ N indicates the number of orbits around the earth when the tribe moves 100 or 98 kilometers along the latitude. But in order for the earth to be orbited at least once, the tribe must be in a distance less than 1 0 0 km / 2 π ≈ 1 6 km to the north pole. Thus, in the southern route at a distance of more than 100 km from the pole, there can be no orbiting so that n = 0 . Since we are close to the pole, the latitude is nearly 90 degrees, so that ϕ = π / 2 − δ with a small angle δ . With the help of the small angle approximation cos ( π / 2 − δ ) = sin ( δ ) ≈ δ then follows 1 0 0 km 9 8 km ≈ 6 3 7 1 km ⋅ δ Δ λ ≈ 6 3 7 1 km ⋅ ( δ − 0 . 0 1 5 7 ) ( Δ λ + 2 π m ) For example, for m = 1 we get a solution with δ ≈ 0 . 0 1 7 8 ≈ 1 ∘ and Δ λ ≈ 0 . 8 7 9 ≈ 5 0 ∘ , so that ϕ ≈ 8 9 ∘ would be an alternative solution for the problem. For higher values m > 1 , we must move even closer to the north pole, while the angle δ from point A to the north pole must be at least 0.9 degrees. Therefore, for all alternative solutions, the value is rounded value of the latitude is ϕ ≈ 8 9 ∘ .
I agree with you, in addition to the value ϕ ≈ 5 2 ∘ is ϕ ≈ 8 9 ∘ an another, mathematically possible solution, even if it does not make much sense in reality.
Cool problem. Curiously, the radius of the earth doesn't matter to the East and West distances. We just use their ratio. (We do need it to establish the angle covered North to South.)
I have a question. What if we try to solve this problem without aproximation. I mean tan − 1 ( sin ( 6 3 7 1 1 0 0 ) ( cos ( 6 3 7 1 1 0 0 ) − 0 . 9 8 ) ) My calculation shows that it's 89.215. So what's wrong ?
Log in to reply
I have the same problem with you, it seems that when the angle gets smaller, the differences between the approximation and the exact equation gets higher :(
Log in to reply
Yeah... i guess it means the answear 52 is incorrect. If we however want to approximate sin(x) in this case we should use not only the first term of the Maclaurin series but the whole series 6 3 7 1 1 0 0 − 3 ! ( 6 3 7 1 1 0 0 ) 3 + 5 ! ( 6 3 7 1 1 0 0 ) 5 − 7 ! ( 6 3 7 1 1 0 0 ) 7 + 9 ! ( 6 3 7 1 1 0 0 ) 9 − 1 1 ! ( 6 3 7 1 1 0 0 ) 1 1 . . . , calculate O(x^(2n+1)) that is depend on our needeness (in theory the error of solution should be less or much more less then the error of input data) and only after that apply constructed approxomattion.
The reason is probably, that your calculator is set to measure all angles in degrees. Here's my calculation, I always use the unit radian (the small angle approximation for sinus and cosine work only in this case). If you want to get the correct result, you have to enter the correct angle Δ ϕ = 0 . 9 ∘ instead of Δ ϕ = 1 0 0 / 6 3 7 1 radians .
Log in to reply
Omg, thank you. haha i feel very stupid right now.
Of course I would go and calculate the complementary angle of 37°...
Sir , Could I solve this by taking the help of standard Spherical Coordinates....r,phi and Theta
Log in to reply
Sure. I is just a different way to label the angles.
As the travel at constant longitude is along a geodesic, both cover an angle Δ ϕ such that Δ ϕ ⋅ R = 1 0 0 k m , so Δ ϕ ≈ 0 . 0 1 5 6 9 6
If λ is the angle traveled at constant latitude, we know that the radius of the circle of that latitude is r ϕ = R ⋅ c o s ( ϕ ) , and λ ⋅ r ϕ = 1 0 0 k m , so we have λ = R ⋅ c o s ( ϕ ) 1 0 0 .
We also know that λ ⋅ r ϕ + Δ ϕ = 9 8 k m , which simplifies into c o s ( ϕ ) c o s ( ϕ + Δ ϕ ) = 1 0 0 9 8
7 steps of a dichotomic search for ϕ in the range [ 0 , π / 2 ] yields an approximate value of 5 1 . 7 .
The latitude, ϕ , is the angle above the equator from Earth's center. Thus, we know that an arc traversed at constant longitude (along a meridian) is always of length R Δ ϕ .
The longitude, θ , is the angle from the prime meridian to other meridians, as measured from Earth's axis. The distance from any point on Earth's surface to its axis is R cos ϕ , and hence the length of any arc traversed at constant latitude (parallel to the equator) is always of length R cos ϕ Δ θ .
Let a = 1 0 0 k m , b = 9 8 k m , and ϕ 0 be the latitude at A . Then we may immediately write Δ ϕ = R a , and we may determine ϕ 0 as follows: Δ θ = R cos ϕ 0 a cos ( ϕ 0 + R a ) cos ϕ 0 cos R a − sin ϕ 0 sin R a cos ϕ 0 ( cos R a − a b ) tan ϕ 0 ϕ 0 = R cos ( ϕ 0 + R a ) b = a b cos ϕ 0 = a b cos ϕ 0 = sin ϕ 0 sin R a = cot R a − a b csc R a = arctan ( cot R a − a b csc R a ) ≈ 0 . 9 0 2 4 r a d ≈ 5 1 . 7 0 4 1 ∘
I'm going to stick to wood working
As the arcs of the circles of latitude trailed in spring and in autumn differ by 2%, their radii will do so as well.
This difference 0 . 0 2 R cos ϕ is one leg of a right-angled triangle, the hypotenuse is the summer trail=100, and the angle is ϕ ,
yielding: sin ϕ = 0 . 0 2 R cos ϕ / 1 0 0 , tan ϕ = 0 . 0 2 ∗ 6 3 7 1 / 1 0 0 = 1 . 2 7 4 2 ϕ = 5 1 . 8 7 5 °
The metric on the sphere of radius R can be written as d S 2 = R 2 d θ 2 + R 2 sin 2 θ d ϕ 2 , θ ∈ [ 0 , π / 2 ] , ϕ ∈ [ 0 , 2 π ] We have to note that we start counting the angle θ from the north pole up to the equator. Angle ϕ doesn't have a particular point, and we can start counting from wherever we please. The nomads start from ( θ 0 , 0 ) in our choice of coordinates. After the first journey they end up at ( θ 0 , ϕ 0 ) . The proper distance is given by 1 0 0 = ∫ 0 <span class="mord
The position on the surface of the earth is determined by latitude ϕ and longitude λ . While the circles of longtitude go from pole to pole and have a radius R equal to earth's radius, the radius R ′ = R cos ϕ of the circle of latitude depends on the latitude ϕ and becomes smaller towards the pole. If the nomadic tribe travels along a circle about the angle Δ ϕ or Δ λ , the distance traveled results to Δ s = R Δ ϕ and Δ s = R ′ Δ λ , respectively.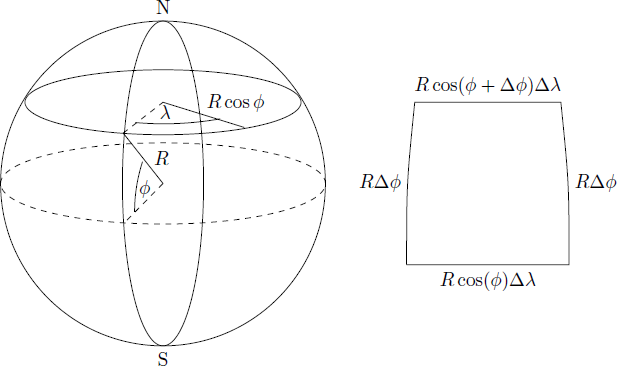
Therefore, for individual sections of the route follows 1 0 0 km 1 0 0 km 9 8 km = R cos ( ϕ A ) Δ λ = R Δ ϕ = R cos ( ϕ A + Δ ϕ ) Δ λ where ϕ A is the latitude of the winter quarter and Δ ϕ = 1 0 0 km / 6 3 7 1 km ≈ 0 . 0 1 5 7 ≈ 0 . 9 ∘ is the covered latitude. Therefore, 1 0 0 km 9 8 km = 0 . 9 8 ⇒ ϕ A = cos ( ϕ A ) cos ( ϕ A + Δ ϕ ) = cos ( ϕ A ) cos ( ϕ A ) cos ( Δ ϕ ) − sin ( ϕ A ) sin ( Δ ϕ ) ≈ cos ( ϕ A ) cos ( ϕ A ) − Δ ϕ sin ( ϕ A ) = 1 − Δ ϕ tan ( ϕ A ) ≈ arctan ( Δ ϕ 0 . 0 2 ) ≈ 0 . 9 0 5 ≈ 5 1 . 9 ∘ Here we used the addition theorem for the cosines and the small angle approximations cos Δ ϕ ≈ 1 and sin Δ ϕ ≈ Δ ϕ . A more accurate evaluation results Δ ϕ A = 5 1 . 7 ∘ .