Non Consecutive letters
How many ways are there of choosing three different letters from { A , B , C , D , E , F , G , H , I , J } so that no two of the letters are consecutive?
The answer is 56.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Since the order of the chosen letters is immaterial, we can choose 3 letters and arrange them in alphabetical order in 1 way. Now we consider a 10 number sequence consisting of 0's and 1's with a 0 for a letter appearing in the selection and a 1 otherwise. for example: for the selection [ACD] we define the sequence to be [0100111111]. since for different selections we have different sequences, and every such sequence corresponds to a unique selection (the letters are arranged in alphabetical order), we have established a bijection to the number of ways of arranging 3 0's and 7 1's such that no 2 0's are consecutive. To satisfy the condition we begin with 01010 and the answer reduces to the number of ways of putting 5 identical 1's in the 4 places, which by the stars and bars technique, can be done in 8C3 =56 ways.
First count how many ways are of choosing three different letters so that two or more of the letters are consecutive. There are two cases.
Case 1: The three letters are consecutive
(slide parenthesis)
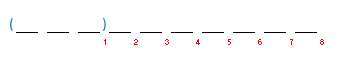
8 ways
Case 2: Two letters are consecutive
a ) The 2 letters are in the edge ⇒ can be combined with 7 letters
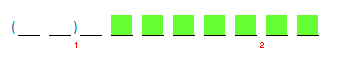
1 4 ways
b ) The 2 letters are not in edge ⇒ can be combined with 6 letters (slide parenthesis and green squares)
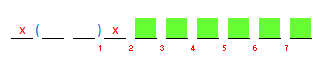
4 2 ways
Then, do inclusion- exclusion:
ways of choosing three letters-last cases
( 3 7 ) − 8 − 1 4 − 4 2 = 5 6 ways
Going from left to right, let a be the number of letters prior to the "first" of the three letters chosen, b be the number of letters between the first and second letter chosen, c be the number of letters between the second and third letter chosen and d the number of letters after the third letter chosen.
Since 7 letters are not chosen, we then need to find the number of solutions to the equation a + b + c + d = 7 , where a , b , c , d are integers such that a , d ≥ 0 and b , c ≥ 1 . (This last condition is to ensure that no two of the letters are consecutive.)
Now let b ′ = b − 1 and c ′ = c − 1 . This then gives us the equation
a + b ′ + c ′ + d = 5 where a , b , c , d are non-negative integers.
This is now a stars and bars equation, which according to theorem two in the link has
( 5 5 + 4 − 1 ) = ( 5 8 ) = 5 6 solutions.