Non-Funzione di Cardano
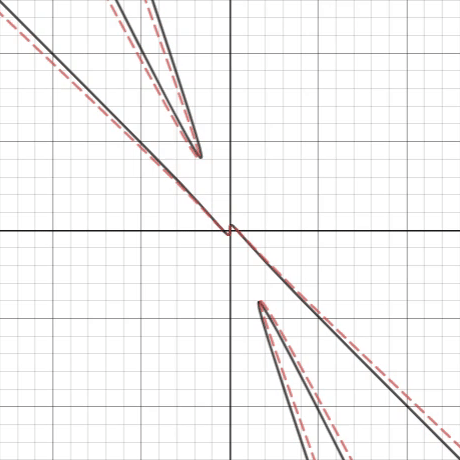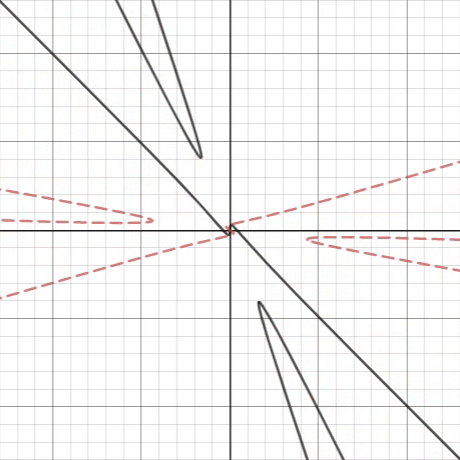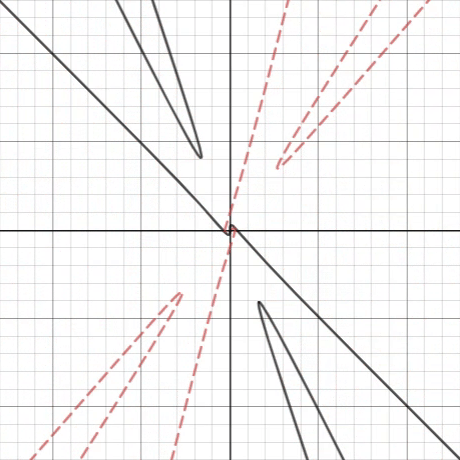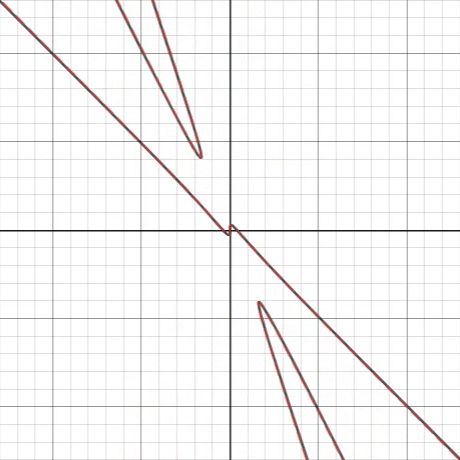
As indicated by the black line, the graph at radians (the initial position before the rotation) is a function at some interval as there exists a vertical line, crossing it once. If we rotate it counterclockwise, for some interval , where and are respectively infimum and supremum , the image is nowhere a function.
If the absolute value of the range difference can be expressed as
where are positive integers and is square free, input the product as your answer.
The answer is 140.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Firstly, let's convert to polar coordinates:
r 3 ( 6 cos 3 ϕ ) + 1 1 cos 2 ϕ sin ϕ + 6 cos ϕ sin 2 ϕ + 3 sin 3 ϕ = r cos ϕ
r 2 ( 6 + 1 1 tan ϕ + 6 tan 2 ϕ + tan 3 ϕ ) = cos 2 ϕ 1
Now, that was when θ = 0 . When we start to rotate then:
r 2 ( 6 + 1 1 tan ( ϕ − θ ) + 6 tan 2 ( ϕ − θ ) + tan 3 ( ϕ − θ ) ) = cos 2 ( ϕ − θ ) 1
But what we really interested in are the vertical lines, lets get x value by multiplying by cos 2 ϕ :
x 2 ( 6 + 1 1 tan ( ϕ − θ ) + 6 tan 2 ( ϕ − θ ) + tan 3 ( ϕ − θ ) ) = cos 2 ( ϕ − θ ) cos 2 ϕ
For comfort, let ϕ ˉ = ϕ − θ :
x 2 ( 6 + 1 1 tan ϕ ˉ + 6 tan 2 ϕ ˉ + tan 3 ϕ ˉ ) = cos 2 ϕ ˉ cos 2 ( ϕ ˉ + θ )
A few trigonometrical operations on the right part and:
x 2 ( 6 + 1 1 tan ϕ ˉ + 6 tan 2 ϕ ˉ + tan 3 ϕ ˉ ) = ( cos θ − sin θ tan ϕ ˉ ) 2
Again, purely for comfort, let t = tan ϕ ˉ :
x 2 ( 6 + 1 1 t + 6 t 2 + t 3 ) = ( cos θ − sin θ t ) 2
x 2 = ( 6 + 1 1 t + 6 t 2 + t 3 ) ( cos θ − sin θ t ) 2
x 2 = ( t + 1 ) ( t + 2 ) ( t + 3 ) ( cos θ − sin θ t ) 2
Now let's review what we've got: a relation between x and t . If we have two different values of t that result in the same ∣ x ∣ that would mean that we at least two points in the vertical line. So, we need to find such θ so that for any x there'll be several values of t .
Let's consider curve ( t + 1 ) ( t + 2 ) ( t + 3 ) 1 . Areas ( − ∞ ; − 3 ] and [ − 2 ; − 1 ] are unavailable since the function is negative and x 2 can't be negative. What's left is intervals ( − 3 ; − 2 ) and ( − 1 ; + ∞ ) .
The act of multiplication by ( cos θ − sin θ t ) 2 "pulls" the curve to the x-axis line (since the function is zero when t = tan θ 1 ). So if we "pull" the "parabola" above the interval ( − 3 ; − 2 ) we'll achieve what we need. So, the condition is:
− 3 < tan θ 1 < − 2
3 1 < tan θ < 2 1
arctan 3 1 < θ < arctan 2 1
Thus, ∣ a − b ∣ = arctan 2 1 − arctan 3 1 = arctan 7 1 , or alternatively ∣ a − b ∣ = 2 arctan ( 5 2 − 7 ) .
P.S.: the unclear part is whether you can "pull" in ( − 1 ; + ∞ ) . Seems like a no, the resulting "bump" won't be high enough to reach the minimum in ( − 3 ; − 2 ) but I got the answer and am not motivated to prove it.
P.S.S.: the last bit w/ arctan is sly, not gonna lie) . Also sorry for absence of graphs