Non-Homogenous Seesaw
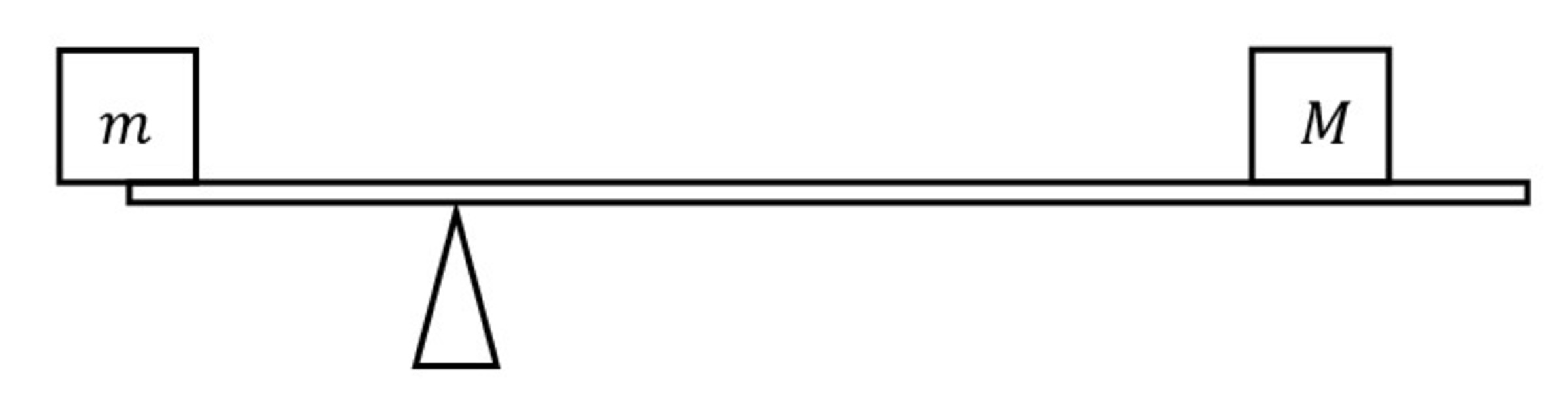 A non-homogenous seesaw has a length of 1.5 m. 2 objects with masses
and
= 3 kg are put on the seesaw.
is put 20 cm from the support while
is put 1.2 m from the support. Calculate the magnitude of the force (in newtons) exerted by the support if the seesaw is in equilibrium. (Round to the nearest integer)
A non-homogenous seesaw has a length of 1.5 m. 2 objects with masses
and
= 3 kg are put on the seesaw.
is put 20 cm from the support while
is put 1.2 m from the support. Calculate the magnitude of the force (in newtons) exerted by the support if the seesaw is in equilibrium. (Round to the nearest integer)
Linear Mass Density for the seesaw : =
Acceleration of Gravity :
The answer is 261.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let m be x = 0. First, we need to find the centre of mass of the seesaw.
x C O M = ∫ 0 1 . 5 x 2 d x ∫ 0 1 . 5 x 3 d x = 1 m from m
The total mass of the seesaw :
m s e e s a w = ∫ 0 1 . 5 x 2 d x = 8 9 kg
Equilibrium of Torques :
Σ τ = 0
m . 5 1 = 3 . 1.2 + 8 9 . (1-0.2)
m = 22.5 kg
Equilibrium of Forces :
N = (22.5 + 3 + 8 9 ) kg . 9 . 8 s 2 m
N ≈ 261 N