Non-standard Weights

Logic Level 2

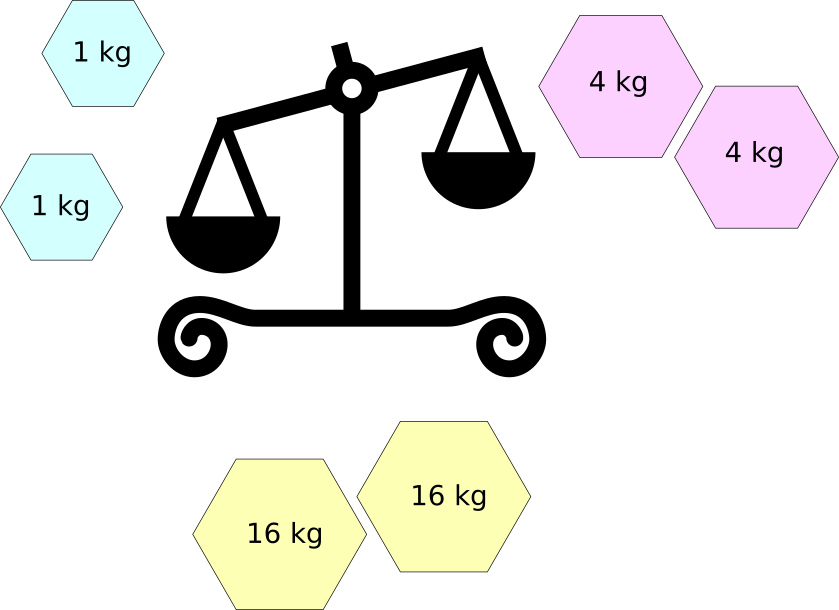
You have a pan balance, and two weights of $1\text{ kg}, 4\text{ kg}$ and $16\text{ kg}$ each.

How many different positive weights can you measure using just these given weights?

As an explicit example, it is possible to measure 3 kg using these weights. Place a $4\text{ kg}$ weight on one pan, and a $1 \text{ kg}$ weight on the other pan. Only an object weighing 3 kg will be able to balance the pans.

The answer is 42.

1 solution

Pranshu Gaba
May 11, 2016

All weights from 1 kg to 42 kg can be measured using the given weights. Try to prove it!

Claim: Any positive integer can be written in the form of $a_0 \times 4^0 + a_1 \times 4^1 + a_2 \times 4^2 + \cdots + a_n \times 4^n$ for $a_i \in \{ -1, 0, 1, 2\}$ and for sufficiently large $n$ .

Well , to do that you can consider all the possible weights from 1 to the maximum weighting that can be obtained that being the weighting that takes all the weights on a scale (42 kg) as being in one of the form 4a , 4a+1 , 4a+2 or 4a+3. It can be observed that since the weights have two 4's and two 16 , 16 being 4 * 4 all the multiples until the maximum multiple that can be obtained using them are reachable by either just adding the weights or in the case where the addition will leave some gaps between multiples that aren't covered by using subtraction therefore all weightings of the form 4a being possible. Observe further that since all 4a's are possible all 4a+1 and 4a+2 are also possible since in order to achieve it you would just have to add either a weight or two weights of 1kg. Finally , there remains the case of 4a+3 which can be obtained from any multiple of 4a also since any 4a+3 is a 4a-1 and a 4a-1 can be obtained by inserting on the opposite scale of the 4a kg that have been weighted one of 1kg getting therefore to the conclusion that they can all be generated as the difference between the weights is appropriate. In short , what actually makes possible to have all these weightings is the fact that all the weights that are being used cover by the relation of their differences the possible distribution of 4 between the values. It can be said that by making a statement on this way it is expressed synthetically what represents all the cases considered anyways.

A A - 5 years, 1 month ago

Non-standard Weights

The answer is 42.

1 solution

0 pending reports