None of My Business?
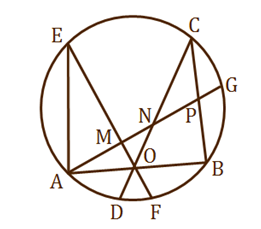
As shown in the diagram above,
,
,
are chords in a circle so that
is parallel to
.
is the midpoint of
,
is the midpoint of
.
Chord
passes through
.
Chord
passes through
, and intersects
at
.
Chord
passes through
, and intersects
at
.
If the area of
is 15 units and that of
is 10 units.
Find the diameter of the circle given that it is an integer.
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Lemme tell u a secret... A B C E is actually a parallelogram . Sounds peculiar? Lemme show you...
Set the above figure onto a complex plane with A B as the real axis and A be the origin, the points A , B , C , E , M , N , O and P are represented by complex numbers a , b , c , e , m , n , o and p respectively (the e here is not the constant 2 . 7 1 8 2 8 … , don't be confused! I won't be using that constant here).
Let's set o = 1 , then b = 2 . Suppose to get to P from B we go x units along the real axis and 1 unit up the imaginary axis, then p = 2 + x + i , thus c = 2 + 2 x + 2 i . ∴ B C = c − b = 2 x + 2 i ∴ C O = o − c = − ( 1 + 2 x ) − 2 i
Since A E ∥ B C and ∣ A B ∣ = 2 , thus e = k 0 x + k 0 i for some value k 0 ∈ R .
Let's first find the value of n . Since n = c + C N , suppose n = k 1 p and C N = k 2 C O = − k 2 ( 1 + 2 x ) − 2 k 2 i where k 1 , k 2 ∈ R .
We have k 1 p = c − k 2 ( 1 + 2 x ) − 2 k 2 i k 1 ( 2 + x ) + k 1 i = 2 + 2 x − k 2 ( 1 + 2 x ) + 2 ( 1 − k 2 ) i
Equating the coefficients of the imaginary part, we have k 1 = 2 ( 1 − k 2 ) .
Equating the coefficients of the real part and substituting k 1 = 2 ( 1 − k 2 ) , we have k 1 ( 2 + x ) = 2 ( 1 − k 2 ) ( 2 + x ) = 2 + 2 x − k 2 ( 1 + 2 x ) 4 + 2 x − 4 k 2 − 2 k 2 x = 2 + 2 x − k 2 − 2 k 2 x 4 − 4 k 2 = 2 − k 2 ∴ k 2 = 3 2 ∴ k 1 = 2 ( 1 − 3 2 ) = 3 2 ∴ n = 3 2 p
Denote S a shape as the area of a shape, since ∣ A N ∣ ∣ A M ∣ = S △ A M O + S △ N O M S △ A M O = 5 3 , thus m = 5 3 n = 5 2 p = 5 4 + 5 2 x + 5 2 i
Now, because o = e + E O , suppose E O = k 3 M O where k 3 ∈ R , then o = 1 = e + k 3 ( o − m ) = k 0 x + k 0 i + k 3 ( 1 − 5 4 − 5 2 x − 5 2 i ) = k 0 x + k 0 i + 5 1 k 3 − 5 2 k 3 x − 5 2 k 3 i = ( k 0 − 5 2 k 3 ) x + 5 1 k 3 + ( k 0 − 5 2 k 3 ) i
By equating the coefficients again we get k 0 = 5 2 k 3 and ( k 0 − 5 2 k 3 ) x + 5 1 k 3 = 1 which we can get k 3 = 5 which in turn implies k 0 = 2 .
Thus, e = A E = k 0 x + k 0 i = 2 x + 2 i = B C , which implies that E C ∥ A B , A B C E is a parallelogram.
Now we have proven that A B C E is a parallelogram, the only circumscribed parallelograms are rectangles, so A B C E must be a rectangle. Let's calculate the area of this rectangle.
∵ ∣ A B ∣ = 2 ∣ A O ∣ ∴ S △ A B N = 2 S △ A O N = 2 × ( 1 0 + 1 5 ) = 5 0 ∵ ∣ n ∣ = 3 2 ∣ p ∣ ∴ S △ A B P = 2 3 S △ A O N = 2 3 × 5 0 = 7 5 ∴ S A B C E = 4 S △ A B P = 4 × 7 5 = 3 0 0 = A B × B C
300 can be factorised as 1 × 3 0 0 2 × 1 5 0 3 × 1 0 0 4 × 7 5 5 × 6 0 6 × 5 0 1 0 × 3 0 1 2 × 2 5 1 5 × 2 0
Since the diameter of the circle is an integer, and the diameter of the circle is A B 2 + B C 2 , we see that only 15 and 20 satisfies the problem.
Hence, the diameter of the circle is 1 5 2 + 2 0 2 = 2 5 .