Nonlinear Resistor

Electricity and Magnetism Level 3

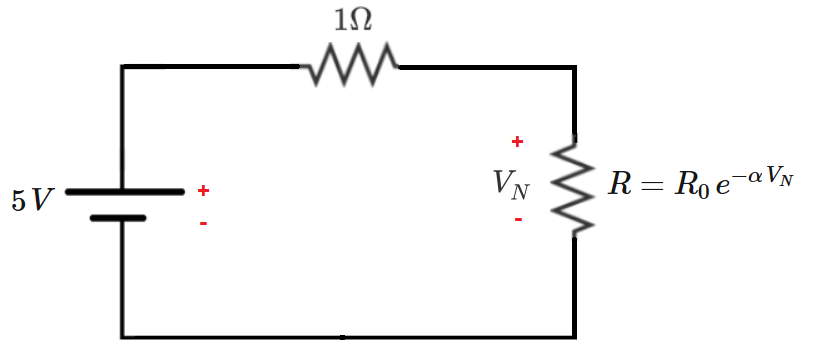
The DC circuit pictured above contains a nonlinear resistor, whose voltage / resistance characteristic is shown.

In this circuit, what resistance value does the nonlinear resistor take in DC steady-state?

Details:
- R 0 = 2 Ω R_0 = 2 \, \Omega
- α = 1 V − 1 \alpha = 1 \, V^{-1}
- Assume that the non-linear resistor obeys Ohm's Law. R = V N I = R 0 e − α V N R = \frac{V_N}{I} = R_0 e^{-\alpha V_N} , where I I is the current


The answer is 0.43709.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Steven Chase
Feb 10, 2018

Current in the circuit:

I = 5 1 + 2 e − V N = 5 − V N 1 5 = ( 1 + 2 e − V N ) ( 5 − V N ) I = \frac{5}{1 + 2\, e^{-V_N}} = \frac{5 - V_N}{1} \\ 5 = (1 + 2\, e^{-V_N})(5 - V_N)

Solve this numerically for V N V_N and then plug back in to get the nonlinear resistance value. It turns out to be about 0.43709 Ω 0.43709 \, \Omega

1 Helpful 1 Interesting 1 Brilliant 0 Confused

I just stumbled upon this problem and I got it wrong. My thoughts on the concept of this problem are as such:

  • When I think of a nonlinear resistance, the first thought that comes to mind is that Ohm's law is invalid.

  • I like to think of nonlinear resistance as: R = d V d I R = \frac{dV}{dI} . If I apply the same argument here, I get an expression for V N V_N as a function of I I .

In this problem, I observe that you implicitly assumed that Ohm's law is valid. Why does this assumption hold true?

Karan Chatrath - 6 months ago

Log in to reply

I simply conceived of it as having those properties. I probably should have stated that it obey's Ohm's Law. In hindsight, I don't know if anything like this exists in reality. I think what you described is similar to a varistor. The varistor appears to have a fixed V-I characteristic. So I suppose for a varistor, you could sweep V over a range (guess and check), and for each V, there would be a corresponding pre-defined I. And then you could calculate Ohm's Law for the standard resistor (1 ohm) to see if that expression yields the same current as the V-I characteristic did. If so, that is the operating voltage. That would be a good problem.

Steven Chase - 6 months ago

Log in to reply

'Varsitor' sounds like an interesting read. I'll take a look and see if I can cook up a question on it, sometiime.

Karan Chatrath - 6 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...