Normal force
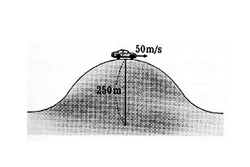 The above picture is a
kg car passing the top of a hill with radius of curvature
m at a speed of
m/s. Find the magnitude of normal force on the car (in N).
The above picture is a
kg car passing the top of a hill with radius of curvature
m at a speed of
m/s. Find the magnitude of normal force on the car (in N).
Gravitational acceleration is m/s .
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The resultant of weight and normal reaction force provides centripetal acceleration to the car towards the center of the curvature.
So, mg-N= m ac, where ac= v^2/r implies mg-N= mv^2/r, so N= m g - m v^2/r = 100 (10- 50^2/250)=0
Normal Reaction = 0N...Hence the passengers inside the car will feel weightless at the top of the trajectory, a condition similar to free fall.