Normally concurrent

Geometry Level 5

The normals to the ellipse $\displaystyle \frac{x^2}{4} + \frac{y^2}{9} =1$ at $\displaystyle (x_k , y_k ) ; k = 1,2,3,4$ are concurrent.

Evaluate: $\displaystyle \sum_{m=1}^4 \sum_{n=1}^4 \frac{x_m }{x_n }$

Details and Assumptions:
The points $(x_k , y_k) ; k =1,2,3,4$ all lie on the given ellipse.

2 solutions

Ujjwal Rane
Dec 11, 2014

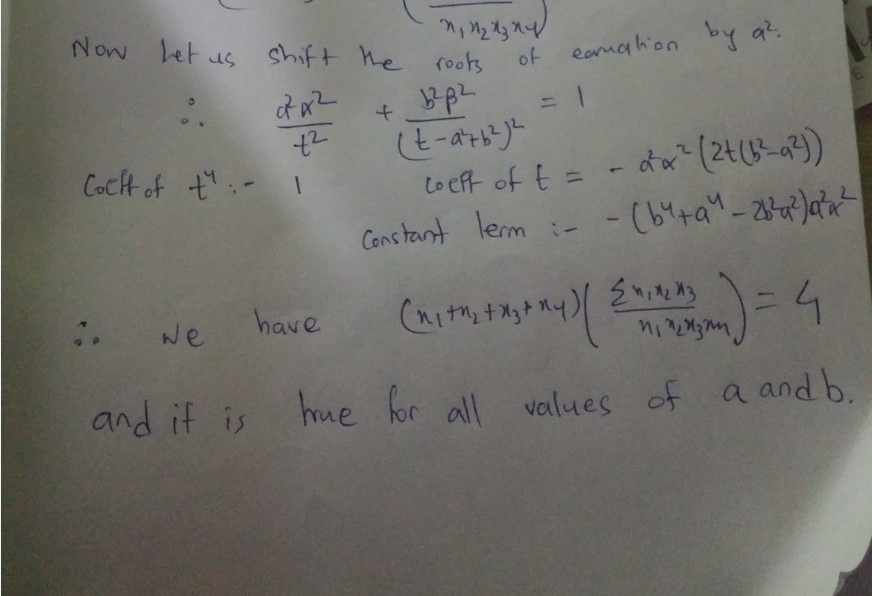
By symmetry the four normals must meet on the major or minor axis.

If they meet on minor axis, the x coordinates of their 'origins' on the ellipse will be ${0, 0, x, -x}$ clearly we cannot take their ratios :-(

So take normals meeting on the major axis. The x coordinates of their 'origins' on the ellipse will be {x, x, -2, 2}

Taking the sums of the sums of their ratios, those with +2 and -2 add up to zero leaving only x/x four times which gives the result $\boxed {4}$ .

Very Nice ! But How can we Proceed if we don't consider effect of Symmetry ? @Ujjwal Rane Sir

Karan Shekhawat - 6 years, 6 months ago

Arghyadeep Chatterjee
Nov 16, 2018