Not 1789 Sangaku Problem :)
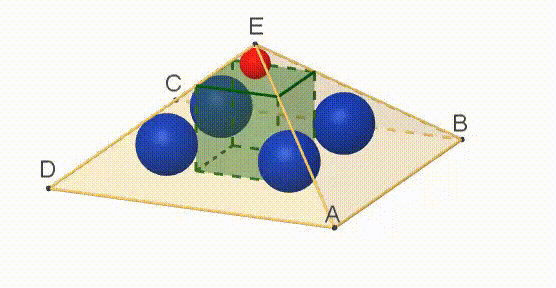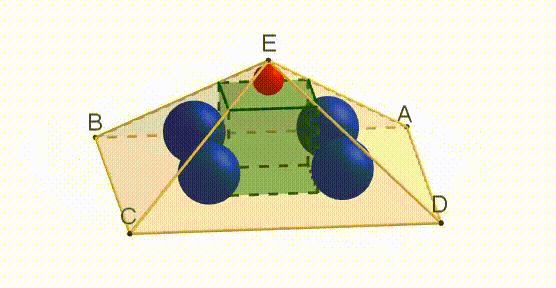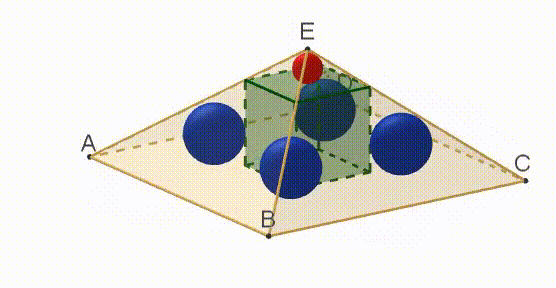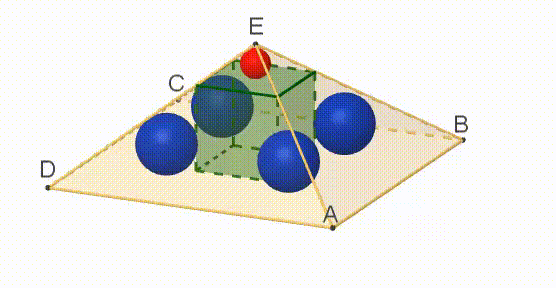
A cube is inscribed in a regular right pyramid with a square base A B C D . Five spheres are inscribed, as shown above. One sphere -the red one on top- touches one face of the cube and the four faces of the pyramid that meet at vertex E . Each of the four blue spheres touches one edge of the cube and the three faces of the pyramid that meet at one of the other vertices, A , B , C and D .
The radius of each blue sphere is twice that of the red sphere.
Find the ratio of the side s of the pyramid’s base to the pyramid’s height h .
If h s = a ⋅ ( b + c − d ) , submit a + b + c + d .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let s be the bottom side of the pyramid, h be the height of the pyarmid, c be the side length of the cube, r be the radius of the small red sphere, and 2 r be the radius of one of the blue spheres, and label the diagram as follows:
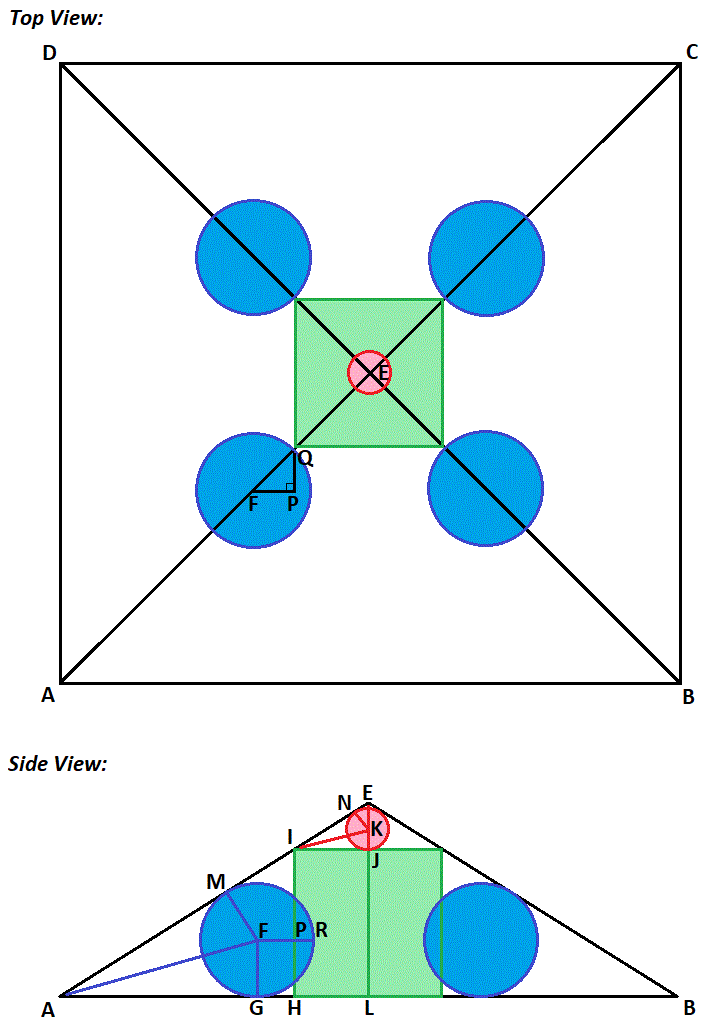
In the top view, △ F P Q is a right isosceles triangle where the hypotenuse F Q = 2 r , so Q P = F P = 2 r .
In the side view (where D is directly behind A and Q is directly behind P ), F P = G H = 2 r .
By similar triangles, let θ = ∠ G A F = ∠ M A F = ∠ J I K = ∠ K I N . Since △ G A F ∼ △ J I K , A G F G = I J K J or A G 2 r = 2 c r , which solves to A G = c .
On △ I H A , tan 2 θ = c + 2 r c . On △ K J I , tan θ = 2 c r = c 2 r . Since tan 2 θ = 1 − tan 2 θ 2 tan θ , c + 2 r c = 1 − ( c 2 r ) 2 2 ( c 2 r ) , which solves to c = ( 2 − 2 2 + 2 ) r , and also means that tan 2 θ = c + 2 r c = 2 − 2 2 + 2 + 2 2 − 2 2 + 2 .
On △ E L A , tan 2 θ = 2 s h , which rearranges to h s = tan 2 θ 2 so that h s = 2 − 2 2 + 2 2 ( 2 − 2 2 + 2 + 2 ) = 2 ( 1 + 2 − 2 ) . Therefore, a = 2 , b = 1 , c = 2 , d = 2 , and a + b + c + d = 7 .
Nice solution David. With a very skilful 3D perception, you just needed a few triangles and some trigonometry to figure out the answer. Thanks for posting.
Let r be the red sphere’s radius and R the radius of each blue sphere.
We take one section through vertex E and the midpoints M and N of A B and C D respectively (figure 1).
Let O be the center of the red sphere, F , P the contact points of the sphere with the cube and the face E C D , E ′ the midpoint of M N and c the edge of the cube.
Then, triangles O P E and E E ′ N are similar, thus E ′ N O P = E N O E ⇔ 2 s r = h 2 + 4 s 2 h − c − r , which solves to r = s + 4 h 2 + s 2 s ( h − c ) ( 1 )
Consider the plane K U V that contains the edge K Q of the cube and is perpendicular to Q A (hence parallel to D B ) (figure 2). It is easy to see that
K
L
D
U
is a parallelogram, since
K
L
∥
D
U
and
K
U
∥
L
D
, thus
A
U
=
s
−
c
,
U
V
=
A
U
2
=
(
s
−
c
)
2
,
K
U
=
L
D
=
K
A
. Hence,
△
K
U
A
is isosceles with base
U
A
=
s
−
c
and height
K
T
=
Q
T
2
+
Q
K
2
=
A
T
2
+
c
2
=
(
2
s
−
c
)
2
+
c
2
.
It is easy to see that
K
L
D
U
is a parallelogram, since
K
L
∥
D
U
and
K
U
∥
L
D
, thus
A
U
=
s
−
c
,
U
V
=
A
U
2
=
(
s
−
c
)
2
,
K
U
=
L
D
=
K
A
. Hence,
△
K
U
A
is isosceles with base
U
A
=
s
−
c
and height
K
T
=
Q
T
2
+
Q
K
2
=
A
T
2
+
c
2
=
(
2
s
−
c
)
2
+
c
2
.
One blue sphere is inscribed in the tetrahedron K U A V .
We know that for the volume of the tetrahedron holds the relation V = 3 1 A ⋅ R ( 2 ) , where A is the total surface area of the tetrahedron and R is the radius of the inscribed sphere.
Now, the volume can also be expressed as V = 3 1 ( area of △ A U V ) ⋅ K Q = 3 1 ⋅ ( 2 1 ( s − c ) 2 ) ⋅ c ⇒ V = 6 1 ( s − c ) 2 ⋅ c ( 3 ) .
For the surface area of the tetrahedron we have:
A = ( area of △ A U V ) + ( area of △ K U V ) + 2 ⋅ ( area of △ K U A ) = 2 1 ⋅ A U ⋅ A V + 2 1 ⋅ U V ⋅ K Q + 2 ⋅ 2 1 ⋅ A U ⋅ K T = 2 1 ⋅ ( s − c ) 2 + 2 1 ⋅ ( s − c ) 2 ⋅ c + 2 ⋅ 2 1 ⋅ ( s − c ) ⋅ ( 2 s − c ) 2 + c 2 ⇒ A = 2 1 ⋅ ( s − c ) ⎣ ⎡ ( s − c ) + 2 ⋅ c + 2 ⋅ ( 2 s − c ) 2 + c 2 ⎦ ⎤ ( 4 ) Combining ( 2 ) , ( 3 ) and ( 4 ) we get R = s − ( 2 − 1 ) c + ( s − c ) 2 + 4 c 2 ( s − c ) ⋅ c ( 5 ) .
Since R = 2 r , from ( 1 ) and ( 5 ) we have s − ( 2 − 1 ) c + ( s − c ) 2 + 4 c 2 ( s − c ) ⋅ c = 2 ⋅ s + 4 h 2 + s 2 s ( h − c ) , which becomes h s + 2 + ( h s ) 2 + 4 h s − h c = 2 ⋅ 1 + 4 ( s h ) 2 + 1 1 − h c ( 6 )
In figure 1, triangles E F K and E E ′ N are similar, hence
F K E ′ N = E F E E ′ ⇔ 2 c 2 s = h − c h ⇔ c = h + s h s ⇔ { h c = h + s s = 1 + h s h s c s = 1 + h s
By denoting h s = x , we get h c = 1 + x x and c s = 1 + x , thus, ( 6 ) consequently becomes x + 2 + x 2 + 4 x − x + 1 x = 2 ⋅ 1 + x 2 4 + 1 1 − x + 1 x ,
which simplifies to ( x − 2 ) x 2 + 4 = 2 x + 2 2 − x 2 ( 7 )
Squaring both sides, we come to the quadratic ( 1 + 2 ) x 2 − 2 ( 2 + 2 ) x + 2 = 0 ( 8 )
The roots of ( 8 ) are x = 2 ( 1 ± 2 − 2 ) . From these two, 2 ( 1 + 2 − 2 ) is the only one that satisfies ( 7 ) , hence h s = x = 2 ( 1 + 2 − 2 ) .
For the answer, a = 2 , b = 1 , c = 2 , d = 2 , thus a + b + c + d = 7 .