Not a perfect circle!
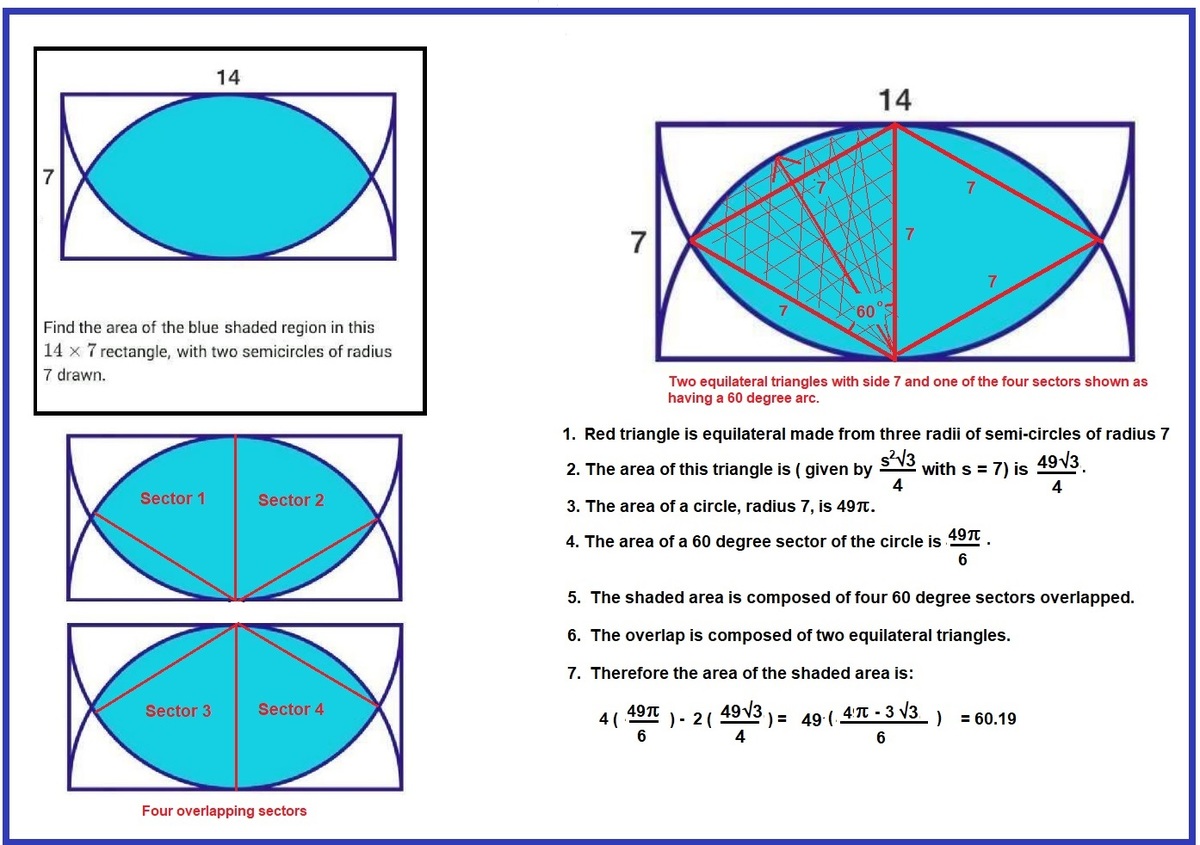
Find the area of the blue shaded region in this 1 4 × 7 rectangle, with two semicircles of radius 7 drawn.
The answer is 60.19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
How did u get 49pi/6? This part is confusing me
Define a coordinate system with (0,0) at the mid-point of the bottom. Then the mid-point of the top is (0,7). The equations of the circles are: (1) x^2 + y^2 = 49, and (2) x^2 + (y - 7)^2 =49, or x^2 + y^2 - 14y + 49 = 49.Cancelling and substituting, we find the circles intersect at y = 7/2, and x = +/- sqrt(147)/2 = +/- 6.062178.. Then the area can be written as 4 integral from x=0 to x = 6.062178 of sqrt(49 - x^2)dx - 4 integral from x =0 to x = 6.062178 of 3.5dx . Carrying out the integration, Area = 60.19. Ed Gray
Draw a line between the intersection points of the two circles, and draw a new half circle with the line on a separate paper. (just one of the half circles) the top part of our newly drawn graph is half of the area of the blue shaded area. We can solve by finding the center of the circle and connect it to the line to make a triangle. The height of the triangle will be 7 / 2 = 3 . 5 , hypotenuse will be 7 . This is one of our familiar 3 0 : 6 0 : 9 0 triangles, the base of our big triangle will be 7 3 × 2 . The obtuse angle of the big triangle will be 1 8 0 − 3 0 − 3 0 = 1 2 0 . The area of our top half circle could be found by subtracting the area of the triangle from the cone π 7 2 × 1 2 0 / 3 6 0 − 7 / 2 × 7 3 × 2 = 3 0 . 0 9 5 The shaded area will be that doubled, which is 6 0 . 1 9
integrating would give perfect answer
Why u have taken obtuse triangle rather u Can do it directly by just using formula of area of circle
Why u have taken the Base radius as 7root2/2
'tis very nice. Very clever, Mas Mus. I struggled with it. Got it wrong three times. Thanks.
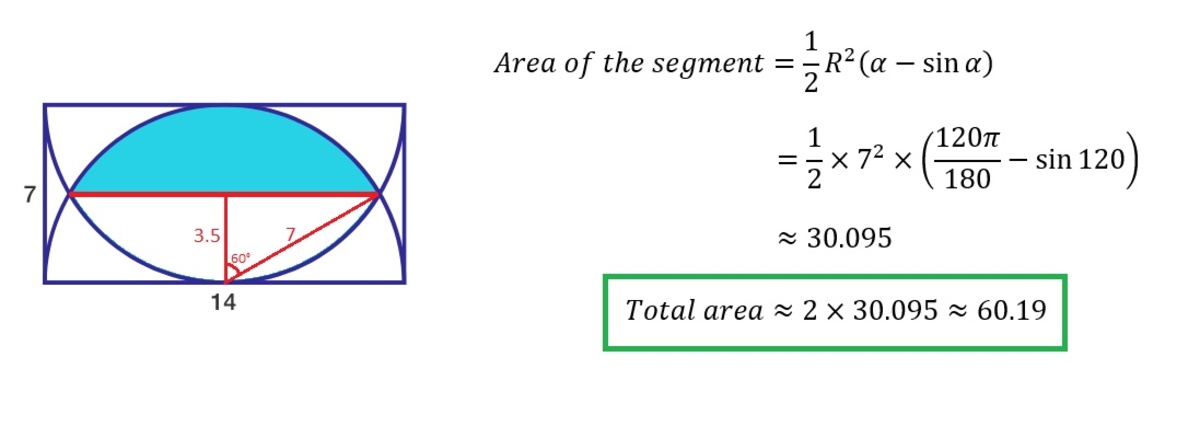
Δ A B C and Δ A C D are two congruent equilateral with side lenght r = 7 . So, the area of Δ A B C = Δ A C D = 4 4 9 3 . The area of sector A B C = 6 4 9 π .
Then, the area of blue shaded region is
2 × 4 4 9 3 + 4 ( 6 4 9 π − 4 4 9 3 ) = 3 9 8 π − 2 4 9 3 = 6 0 . 1 9