Not A Telescoping Sum

$\sum _{ k=1 }^{ \infty }{ \left( \frac { 1 }{ 3k-1 } -\frac { 1 }{ 3k } \right) } =\sum _{ k=1 }^{ \infty }{ \int _{ 0 }^{ 1 }{ { (x }^{ 3k-2 }-{ x }^{ 3k-1 }) } dx } \\ =\int _{ 0 }^{ 1 }{ \sum _{ k=1 }^{ \infty }{ { (x }^{ 3k-2 }-{ x }^{ 3k-1 } } )dx } \\ =\quad \int _{ 0 }^{ 1 }{ \frac { x-{ x }^{ 2 } }{ 1-{ x }^{ 3 } } dx } \quad \\ =\quad \frac { ln(3) }{ 2 } - \frac { \sqrt { 3 } \Pi }{ \left( { 3 }^{ 2 } \right) 2 }$

$\begin{aligned} S &= \sum_{k=1}^\infty \left( \frac{1} {3k-1}- \frac{1} {3k} \right) \\ & = \sum_{k=1}^\infty \frac{2\sin \left( (k-1)\frac {2 \pi}{3}\right)} {\sqrt{3} k} \quad \quad \small \color{#3D99F6}{\text{See Note.}} \\ & = \Im \left[ \frac {2 e^{-i\frac {2\pi} {3}}} {\sqrt {3} } \sum_{k=1}^\infty \frac {e^{i\frac {2 k \pi} {3}}}{k} \right] \\ & = \Im \left[ - \frac {2 e^{-i\frac {2 \pi} {3}}} {\sqrt {3} } \ln (1 - e^{i\frac { 2 \pi} {3}}) \right] \\ & = \Im \left[ - \frac {2} {\sqrt {3} } \left(-\frac {1} {2} - i\frac {\sqrt {3}} {2} \right) \ln \left(\frac {3} {2} - i\frac {\sqrt {3}} {2} \right) \right] \\ & = \Im \left[ \left(\frac {1} {\sqrt{3}} + i \right) \ln \left(\sqrt{3} \left(\frac {\sqrt {3}} {2} - i\frac {1} {2} \right)\right) \right] \\ & = \Im \left[ \left(\frac {1} {\sqrt{3}} + i \right) \ln \left(\sqrt{3} e^{-i\frac {\pi}{6}} \right) \right] \\ & = \Im \left[ \left(\frac {1} {\sqrt{3}} + i \right) \left(\frac {\ln 3}{2} -i\frac {\pi}{6} \right) \right] \\ & = \frac {\ln 3} {2} - \frac{\sqrt {3} \pi} {18} \end{aligned}$

$\Rightarrow a+b+c+d+e=3+2+3+3+2=\boxed {13}$

Note:

$\begin{aligned} S & = \sum_{k=1}^\infty \left( \frac{1} {3k-1}- \frac{1} {3k} \right) \\ & = \frac 12 - \frac 13 + \frac 15 - \frac 16 + \frac 18 - \frac 19 + ... \\ & = \frac 01 + \frac 12 - \frac 13 + \frac 04 + \frac 15 - \frac 16 + \frac 0 7 + \frac 18 - \frac 19 + ... \\ & = \frac 2{\sqrt 3} \left(0 \cdot \frac 11 + \frac{\sqrt 3}2 \cdot \frac 12 - \frac{\sqrt 3}2 \cdot \frac 13 + 0 \cdot \frac 14 + \frac{\sqrt 3}2 \cdot \frac 15 - \frac{\sqrt 3}2 \cdot \frac 16 + 0 \cdot \frac 17 + \frac{\sqrt 3}2 \cdot \frac 18 - \frac{\sqrt 3}2 \cdot \frac 19 + ... \right) \\ & = \frac 2{\sqrt 3} \left( \sin 0 \cdot \frac 11 + \sin \frac{2\pi}3 \cdot \frac 12 - \sin \frac{4\pi}3 \cdot \frac 13 + \sin 2\pi \cdot \frac 14 + \sin \frac{8\pi}3 \cdot \frac 15 - \sin \frac{10\pi}3 \cdot \frac 16 + \sin 4\pi \cdot \frac 17 + \sin \frac{14\pi}3 \cdot \frac 18 - \sin \frac{16\pi}3 \cdot \frac 19 + ... \right) \\ & = \sum_{k=1}^\infty \frac{2\sin \left( (k-1)\frac {2 \pi}{3}\right)} {\sqrt{3} k} \end{aligned}$

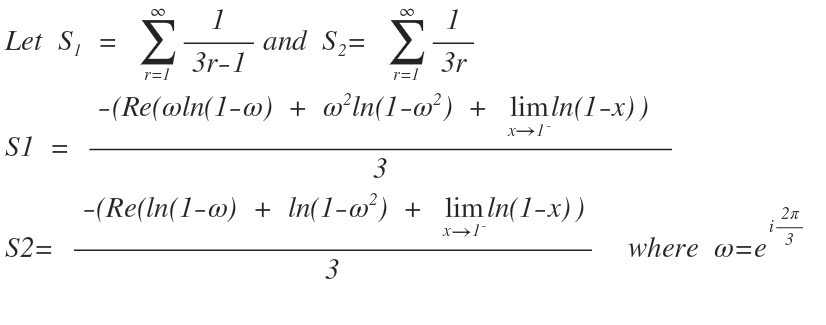
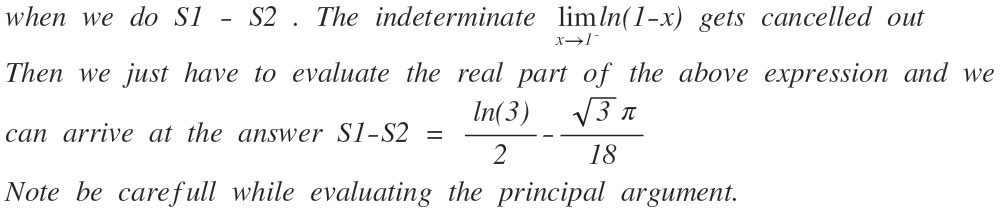
This is not a full solution . The calculation part is left for u guys. I have used taylor series and complex cube root of unity to solve the problem