NOT AND distributivity

Relevant wiki: Truth Tables

An easy way to solve this is to compare input/output tables.

This makes it easy to see that they are not equivalent,​

Relevant wiki: De Morgan's Laws

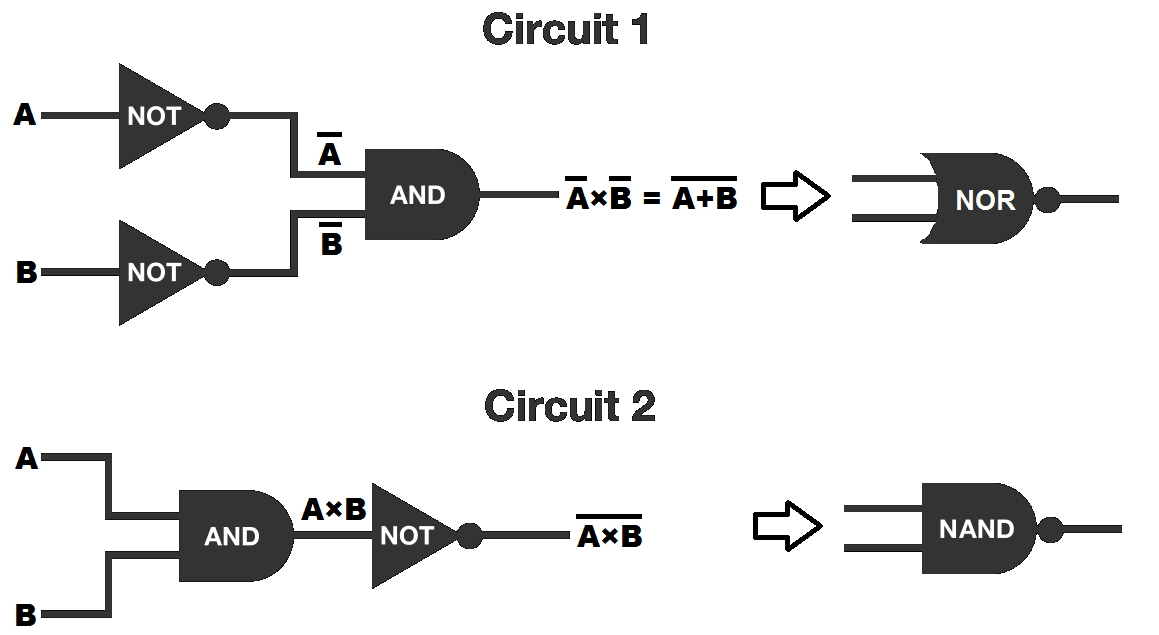
Circuit 1: The input-output table of circuit 1 is as follows:

$\begin{array} {ccc} A & B & Y \\ \hline 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 0 \end{array}$

The input-output table shows that circuit 1 is equivalent to a NOR gate. In Boolean algebra $Y = \overline A \times \overline B$ and by De Morgan's laws , $Y = \overline {A+B}$ .

Circuit 2: The input-output table of circuit 2 is as follows:

$\begin{array} {ccc} A & B & Y \\ \hline 0 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{array}$

The input-output table shows that circuit 2 is equivalent to a NAND gate. In Boolean algebra $Y = \overline {A\times B}$ .

Relevant wiki: Logic Gates

First logic:

$Y = \bar{A} \bar{B}$

Second logic:

$Y = \bar{A B} = \bar{A} + \bar{B}$

In the second logic, the equivalence given is due to DeMorgan's Law. The logics would thus be equivalent if the first logic had an OR gate instead of an AND gate.

Let's denote $\neg A$ as the negation A (i.e. NOT A).

Then, the first diagram corresponds to the logical expression $( \neg A)\wedge(\neg B)$ , while the second corresponds to $\neg (A\wedge B)=( \neg A)\vee( \neg B)$ , where $\wedge$ means AND and $\vee$ means OR.

Then, it is easy to see that the diagrams are different from each other.

NOT(A+B) ≠ NOT(A) + NOT(B)

Let $A, B$ be the two inputs. We claim that $A = 1, B = 0,$ or $A$ is true and $B$ is false, is a counterexample to the statement that the two circuits are equivalent. The first diagram is equivalent to $\neg A \wedge \neg B,$ while the second diagram is equivalent to $\neg(A \wedge B).$ ( $\neg$ represents NOT, while $\wedge$ represent AND.) We have

$\neg A \wedge \neg B = \neg 1 \wedge \neg 0 = 0 \wedge 1 = 0,$

but

$\neg(A \wedge B) = \neg(1 \wedge 0) = \neg 0 = 1.$

Thus, $\neg A \wedge \neg B \neq \neg(A \wedge B)$ for these truth values, so no , the two circuits are not equivalent.

Let's consider the fact that Circuit 2 is a classical NAND gate. With Circuit 1, if the inputs are both equivalent, they will stay equivalent after the NOT gate has been applied to them (0,0 turns to 1,1 and vice versa), and if they are not equivalent, they will stay that way after the NOT gate has been applied to them (1,0 turns to 0,1 and vice versa). With this, we deduce that Circuit 1 is a classical AND gate, which is fundamentally different from a NAND gate, and therefore the circuits are not equivalent.

Consider the possible output of the AND gate in the second circuit. There is only one pair of inputs that result in ON: ON, ON. Because of the next NOT gate, this circuit then results in OFF. There is only one way to get OFF out of the circuit.

Back to the first circuit, the AND gate is last, and there are three pairs of input that will result in OFF; all three of which are possible to output from the individual NOT gates which precede it. There really three ways to output OFF from the second gate. Therefore they are different gates.

If Input 1 and Input 2 are different, then a not gate would not have any effect on the outcome of the and gate. Once one of them goes through a not gate, it makes the outcomes different.

Suppose input 1 as X And input 2 as Y In first circuit we get final output as (X'.Y') While in second we get final output as (X'+Y') So these 2 circuits are not equivalent...

Let INPUT 1 = A
INPUT 2 = B

In circuit 1

  Z= A'.B' = (A+B)'

In circuit 2

  Z= (A.B)'

THUS IN BOTH CASES Z IS NOT EQUAL SO THE TWO CIRCUITS ARE NOT EQUIVALENT

Circuit 1 is 'hard' to turn ON as you have to get both inputs right. Circuit 2 is 'easy' to turn on, because you need OFF to come out of the AND.

The first answers the question "are both inputs false?". The second answers the question "is at least one of the inputs false?".

On Circuit 1, when both of the inputs are off, the AND output is on. In Circuit 2, when both of the inputs are off or either input 1 or input 2 is on, so is the NOT output. When both of the inputs are on, it turns off the output.

Hope that's quite simple, if you just keep the rules in mind. There's a 50-50 chance of them being alike and not depending on values of input A and B. Maths doesn't need huge formulas, just a learning brain, logic and lots of reasoning.