Not Another Triangle Solving Problem!

Geometry Level 5

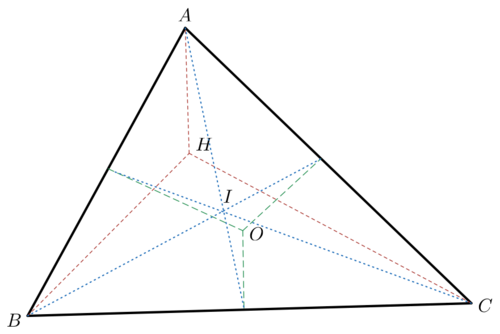$\triangle ABC$ satisfies the following properties:

1) $cosB+cosC=1$

2) $\angle C-\angle B=46^\circ$

Let $O,I,H$ denote the circumcenter, incenter, orthocenter of $\triangle ABC$ respectively. Find $\angle OIH$ in degrees.

1 solution

Lu Chee Ket
Dec 29, 2014

Geometry:

Cos(x + 23 d) = 0.5/ Cos 23 d

B) x = 34.0996083861 d --> 34.1 d

C) x + 46 d = 80.0996083861 d --> 80.1 d

A) 134 d - 2 x = 65.8007832278 d --> 65.8 d

Apply excel to preserve accurate figures.

Solved y = (Tan 34.1 d) x and y = (-Tan 65.8 d) x + Tan 65.8 d gives A(1, 0), B(0, 0) and C(0.766716449455443, 0.519098419260082)

Always take side c and side a only for simple lines' formation, with knowledge of basic mathematics for perpendicular slopes of -1/m:

With mid-point a and mid-point c;

With vertex A and vertex C;

remained:

With vertex B with half angle B and vertex A with half angle A for negative slope:

O(0.5, 0.087267491025666), I(0.678402942126766, 0.208053585174458) and H(0.766716449455443, 0.344563437208749) are obtainable.

Tan P = 1.54574148579832 and Tan Q = 0.677040931662246 imply

Tan (P - Q) = (Tan P - Tan Q)/(1 + Tan P Tan Q) = 0.424474816209606

Obtuse angle = 180 d - (ATan 0.424474816209606)/ Pi * 180 d = 157 d {Exact}

Note: 180 - 46/ 2 = 157 and therefore reasonable to feel confident.