Not As Easy as you think, but still pretty easy

Here is an inaccurate picture of this problem: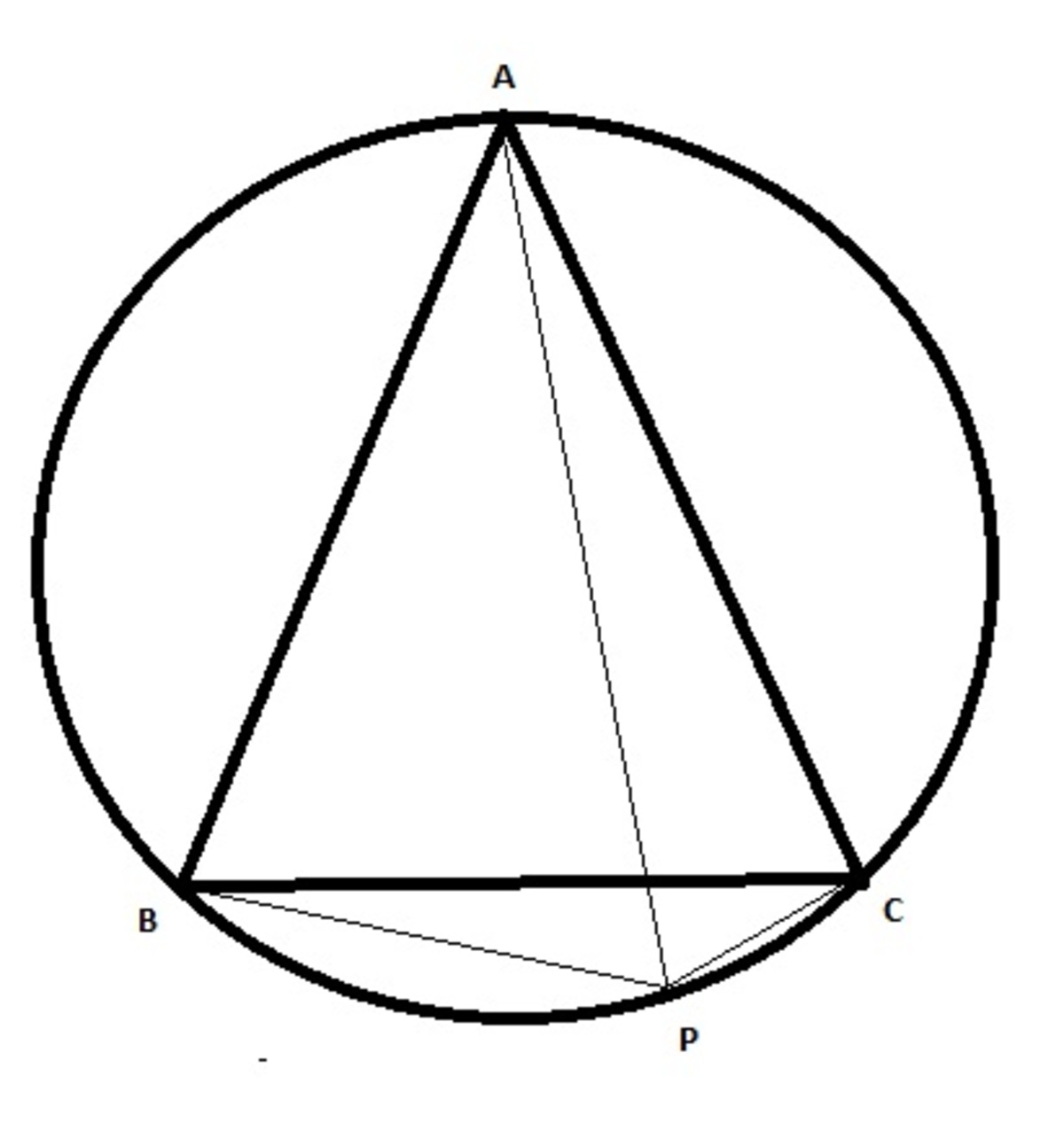

For the moment, and for ease of typing, call the length of PC "x".

The triangle being equilateral works out nicely as it splits the circle into 3 equal minor arcs, each being $\frac{2\pi}{3}$ .

We can use the formula for an inscribed angle to find both angles formed by P:

$m\angle APB=m\angle APC=\frac{1}{2}(\frac{2\pi}{3})=\frac{\pi}{3}$

We now have the two angles above and the lengths of PB and PC. We want the length of AP (call that length "b"). All we are missing is the length of the side of the equilateral triangle (call that length "c"). But maybe we don't need it if we use the Law of Cosines twice.

1) $c^{2}=x^{2}+b^{2}-2xb\cos \frac{\pi}{3}=x^{2}+b^{2}-xb$

2) $c^{2}=5000^{2}+b^{2}-2(5000)b\cos \frac{\pi}{3}=5000^{2}+b^{2}-5000b$

And now we can set equations 1 and 2 equal to one another and solve for b. $x^{2}+b^{2}-xb=5000^{2}+b^{2}-5000b$ $\Rightarrow b=\frac{x^{2}-5000^{2}}{x-5000}=\frac{(x+5000)(x-5000)}{x-5000}=x+5000$ And finally, take that gargantuan number "x", go to the thousand's place and add 5. Luckily the thousand's place is a 0, so all one must do is copy/paste that big number and change one digit, like so: $34691092380932809\color{#D61F06}{5}099$

By Pompeius's Theorem, PA = PB + PC = $\boxed{346910923809328095099}$

Note that the numbers don't really matter in this problem, you just need to add them.

To prove Pompeius's Theorem, just use Ptomely's Theorem.