Where should I look at first?
T
P
is a line that tangent to a circle centered at
O
. If
P
Q
∥
T
O
and
∠
O
T
P
=
2
5
∘
, find the measure of
∠
P
O
Q
in degrees.
Note: The diagram above is not drawn to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
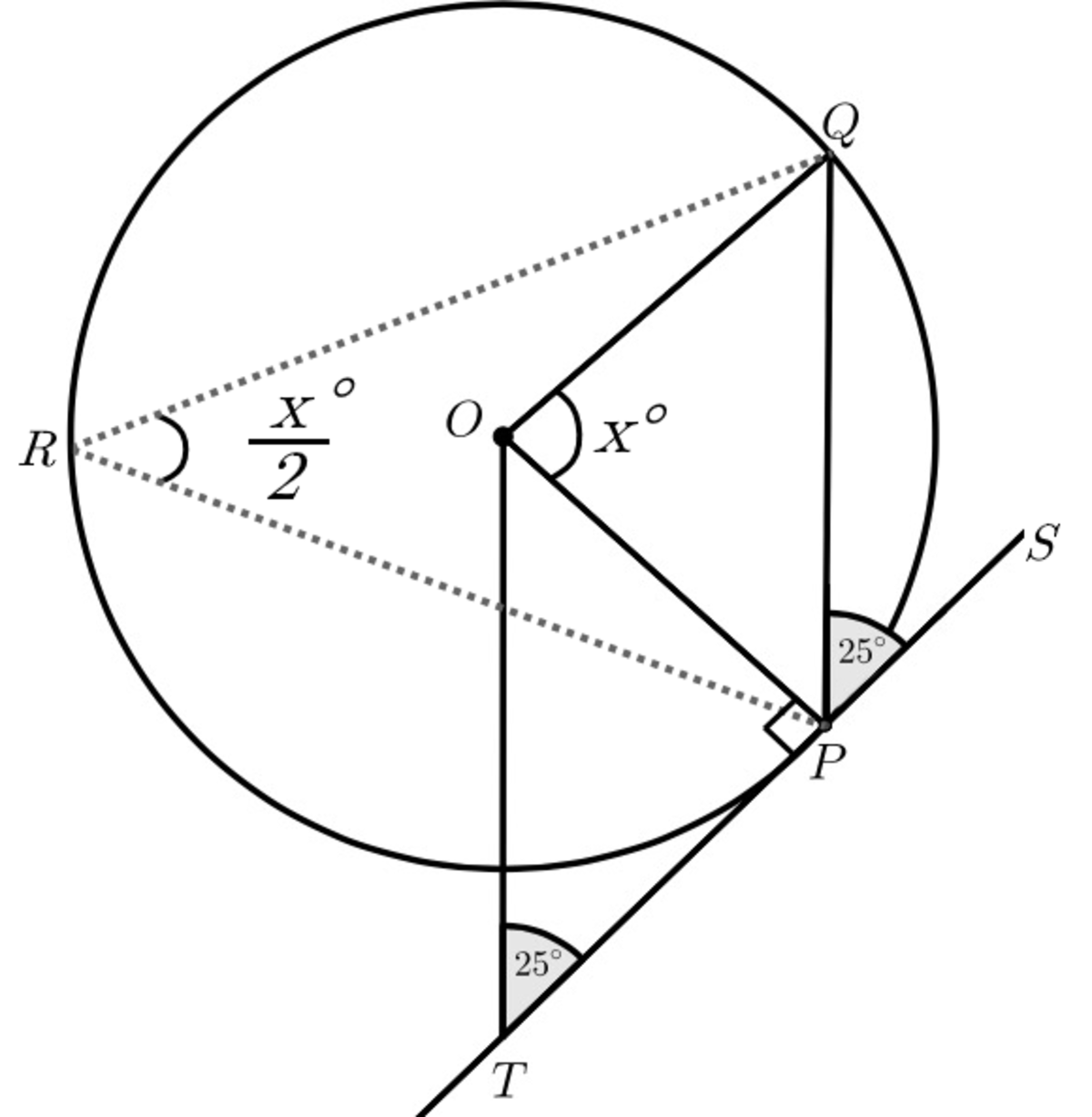 ∠
Q
R
P
=
∠
Q
P
S
⇒
∠
P
O
Q
=
5
0
°
∠
Q
R
P
=
∠
Q
P
S
⇒
∠
P
O
Q
=
5
0
°
It's beautiful
The diagram above is drawn to scale
∠ O P T is obviously 9 0 ∘ because it’s tangent to a circle
∠ T O P = 1 8 0 ∘ − ∡ O T P − ∡ O P T = 1 8 0 ∘ − 2 5 ∘ − 9 0 ∘ = 6 5 ∘
Since P Q is parallel to C D , so we can conclude that ∡ T O P = ∠ O P Q 6 5 ∘ = ∡ O P Q
Since O P and O Q is the same length, we can conclude that ∡ O P Q = ∠ O Q P 6 5 ∘ = ∡ O Q P
Finally, ∠ P O Q = 1 8 0 ∘ − ∡ O P Q − ∡ O Q P = 1 8 0 ∘ − 6 5 ∘ − 6 5 ∘ = 1 8 0 ∘ − 1 3 0 ∘ = ♣ ♠ 5 0 ∘ ♣ ♠
The Spadesuit( ♠ )and the Clubsuit( ♣ ) are just for the decoration. Want more ? :)